9.1.1 Cuantificar la luz
Nota: al tratar de la radiación electromagnética en el espectro visible, se superponen dos ámbitos: El primero se refiere a los aspectos puramente físicos de la cuestión. En este caso las magnitudes y vocabulario utilizados son los propios de la física, objetivos e independientes de la percepción humana. El segundo se refiere a aspectos de la "luz" y del "color"; trata por tanto aspectos subjetivos (percepción humana de la radiación a través del sentido de la vista). En este caso los patrones de medida utilizados, e incluso el vocabulario empleado, están afectados de ciertas correcciones para acercarse a las características muy especiales que tiene la percepción humana de la "luz visible". Como dificultad añadida podemos señalar que el vocabulario utilizado en óptica y fotometría no es en general demasiado consistente.
§1 Medida de la radiación electromagnética
Además de la frecuencia (y longitud de onda) ya señaladas
(![]() H9.1),
existen otras magnitudes significativas en la radiación electromagnética, algunas
especialmente importantes desde el punto de vista óptico. Estas magnitudes están directamente relacionadas con
la percepción que tenemos de la luz.
H9.1),
existen otras magnitudes significativas en la radiación electromagnética, algunas
especialmente importantes desde el punto de vista óptico. Estas magnitudes están directamente relacionadas con
la percepción que tenemos de la luz.
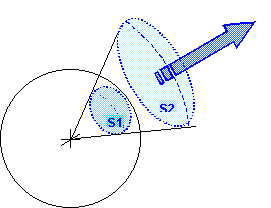
Fig. 2 |
§1.1 Flujo radiante
Las radiaciones electromagnéticas transportan energía, de forma que un objeto luminoso (radiador) emite energía y cualquier objeto iluminado la recibe. La potencia radiante o flujo radiante P es la medida de la cantidad de energía electromagnética que emite un radiador por unidad de tiempo. Se mide en Watt.
La energía transportada puede manifestarse de formas muy diversas en los cuerpos que la reciben: propiciando reacciones químicas (fotosíntesis y bronceado), efectos eléctricos (fotocélulas), efectos mecánicos (viento solar), calentamiento (estufas de infrarrojos), etc.
§1.2 Intensidad radiante
La intensidad radiante Ir expresa la energía emitida por un cuerpo radiante en cada dirección del espacio. Se expresa en Watts/estereoradián (W/sr). Si el radiador emite por igual en todas direcciones y dado que una esfera tiene 4π estereoradianes [3], puede establecerse que un emisor cuyo flujo radiante sea P, produce en sus inmediaciones una intensidad radiante Ir = P / 4π Watt/sr.
§1.3 Densidad de radiación
Los efectos de la radiación electromagnética se expresan mejor en término de la energía emitida (o recibida) por unidad de superficie en unidad de tiempo. En este sentido, más que la potencia radiante del emisor (que puede estar muy alejado) o la intensidad, interesa la densidad de radiación H, que es el valor de la Potencia radiante por unidad de superficie. Se expresa en W / m2.
Conocida la intensidad radiante Ir de un emisor, puede calcularse la densidad de su radiación H a una distancia d:
H = Ir / d2
Como puede verse, la densidad de radiación decrece rápidamente al alejarse del foco emisor (con el cuadrado de la distancia). Por esta razón, los planetas más alejados del Sol son comparativamente más fríos que los más próximos, y la "luz" de una linterna ilumina más intensamente los objetos próximos que los lejanos.
Nota: en el caso de un cuerpo radiante, la densidad de radiación emitida por su superficie se denomina también poder emisivo.(He) Cuando se refiere a la densidad de radiación absorbida por un cuerpo en su superficie, se denomina poder absorbente (Ha).
§2 Medida de la percepción luminosa
Al estar originada por una radiación electromagnética, la intensidad
luminosa no debería ser diferente de la intensidad
radiante ![]() ,
sin embargo, dado que la luz es la percepción humana de la radiación, cuando
se intentan realizar medidas sobre su intensidad (que denominamos brillo)
se presentan dificultades, ya que para una misma intensidad radiante, las
distintas longitudes del espectro visible producen distintas sensaciones de "brillo".
,
sin embargo, dado que la luz es la percepción humana de la radiación, cuando
se intentan realizar medidas sobre su intensidad (que denominamos brillo)
se presentan dificultades, ya que para una misma intensidad radiante, las
distintas longitudes del espectro visible producen distintas sensaciones de "brillo".
Para salvar estas diferencias, la CIE (![]() H9.1) realizó numerosos experimentos en cuanto a la sensación del brillo percibido
por distintos observadores para una misma intensidad radiante en distintas
longitudes de onda (distintos colores). El resultado obtenido se conoce
como eficiencia luminosa del observador estándar, y muestra que la sensación de brillo es
máxima para los colores centrales del espectro (amarillos y verdes), y que
esta sensibilidad decrece rápidamente para los colores extremos (violetas y rojos) [4].
H9.1) realizó numerosos experimentos en cuanto a la sensación del brillo percibido
por distintos observadores para una misma intensidad radiante en distintas
longitudes de onda (distintos colores). El resultado obtenido se conoce
como eficiencia luminosa del observador estándar, y muestra que la sensación de brillo es
máxima para los colores centrales del espectro (amarillos y verdes), y que
esta sensibilidad decrece rápidamente para los colores extremos (violetas y rojos) [4].
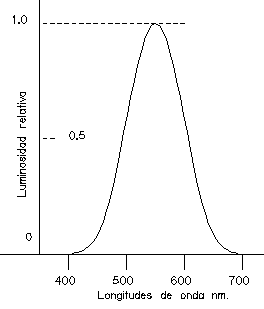 Fig. 3 |
La representación gráfica de la sensación subjetiva de brillo para los distintos colores se denomina curva de luminosidad relativa (fig. 3), en la que puede verse como la sensibilidad máxima corresponde a la radiación de 555 nm de longitud de onda (zona del amarillo), y como tiende asintóticamente a cero a ambos lados del máximo (no es posible poner límites precisos al espectro visible). La escala de ordenadas se ha tomado arbitrariamente igual a la unidad para el máximo de la curva. El valor de la ordenada para cada longitud de onda se denomina coeficiente de luminosidad relativa.
Como consecuencia de lo anterior, cuando el flujo radiante, la intensidad radiante o la densidad de radiación se refieren a la zona visible del espectro, se utilizan magnitudes especiales afectando las anteriores por el coeficiente de luminosidad relativa. Por ejemplo, si se tienen tres tres fuentes luminosas roja R, verde G y azul B, cuyas densidades de radiación respectivas son de igual valor (H), la que parece más luminosa es la verde, después la roja y finalmente la azul. Si queremos expresar la sensación que produce cada una mediante una magnitud que denominaremos L, la densidad H debe estar afectada por un factor de corrección para que corresponda con la sensación que produce. Estas densidades ponderadas serían:
Lg = H * 0.715
Lr = H * 0.213
Lb = H * 0.072
Nota: el problema con este tipo de magnitudes ponderadas es que para que la información sea completa desde el punto de vista físico (objetivo), junto con el valor de magnitud es preciso informar de la longitud de onda de referencia (en nuestro ejemplo suponemos conocidas las longitudes de onda de las fuentes que hemos denominado R, G y B).
§2.1 Flujo luminoso
El flujo radiante ![]() afectado por el coeficiente de luminosidad relativa se denomina flujo luminoso.
La unidad fundamental utilizada en colorimetría es de intensidad
luminosa (ver a continuación), de forma que la unidad de flujo luminoso, denominado lúmen (lm)
se define en función de la unidad de intensidad. lumen
= candela · sr. En la tabla adjunta se muestra un gráfico comparativo de flujos luminosos
afectado por el coeficiente de luminosidad relativa se denomina flujo luminoso.
La unidad fundamental utilizada en colorimetría es de intensidad
luminosa (ver a continuación), de forma que la unidad de flujo luminoso, denominado lúmen (lm)
se define en función de la unidad de intensidad. lumen
= candela · sr. En la tabla adjunta se muestra un gráfico comparativo de flujos luminosos
|
El flujo luminoso también puede ser expresado en unidades absolutas: si consideramos un emisor monocromático de 555 nm cuyo flujo radiante sea de 1 Watt, entonces su flujo luminoso será de 685 lúmenes. En consecuencia el lúmen puede ser definido como el flujo de un emisor monocromático de 555 nm que radiase 1/685 Watt.
Nota: la relación flujo luminoso / flujo radiante de una determinada fuente luminosa se denomina rendimiento luminoso, se expresa en lumen/Watt.
Generalmente el estudio del flujo luminoso de un emisor se realiza dividiendo el espectro visible en 31 zonas, cada una de 10 nm de ancho de banda y midiendo el flujo para la frecuencia media del intervalo. La distribución resultante se conoce como SPD ("Spectral power distribution") y muestra como se distribuye el total de energía irradiada entre las frecuencias del espectro.
En la práctica las fuentes luminosas no son "puras", en el sentido de que no emiten luz de una sola longitud de onda, sino varias, aunque las de una banda determinada puedan ser preponderantes sobre las demás. Un color puro sería aquel cuyo flujo luminoso total estuviese íntegramente contenido en una de las bandas. La proporción de pureza de un color se denomina saturación, intensidad, limpieza o cromaticidad (muy saturado, muy intenso, muy puro, muy limpio o de cromaticidad elevada son expresiones equivalentes en cromatografía). Su contrario es la acromaticidad (insaturación o impureza); se presenta cuando el flujo luminoso se reparte casi por igual en todas las bandas del espectro, lo que origina colores de tonos desvaídos (pastel). El caso extremo de luz perfectamente acromática es cuando el flujo luminoso se reparte exactamente por igual en todas las bandas. En este caso el color varía del negro al blanco a través de la escala de grises.
Nota: la saturación de un color puede definirse como la proporción de color en relación con el brillo, o dicho en términos mas precisos: la proporción de la longitud de onda dominante (color dominante) respecto al total de longitudes de onda que componen el color (que se percibe como brillo). La mínima saturación corresponde al gris neutro que es totalmente insaturado, mientras que la saturación máxima corresponde a los colores puros del espectro. Una forma de disminuir la saturación de un color es añadirle luz blanca (luz de todas las frecuencias); de este modo la frecuencia dominante permanece prácticamente constante mientras que sube el brillo, con lo que la saturación baja.
§2.2 Intensidad luminosa
Cuando la intensidad radiante
![]() se refiere a zonas del espectro visible,
se utiliza una magnitud denominada Intensidad luminosa que se obtiene afectando la intensidad de radiación por
el coeficiente de luminosidad relativa. La intensidad luminosa resulta mucho más adecuada que la intensidad radiante
para los estudios relativos a la luz y el color, porque incorpora la corrección adecuada a la percepción humana.
se refiere a zonas del espectro visible,
se utiliza una magnitud denominada Intensidad luminosa que se obtiene afectando la intensidad de radiación por
el coeficiente de luminosidad relativa. La intensidad luminosa resulta mucho más adecuada que la intensidad radiante
para los estudios relativos a la luz y el color, porque incorpora la corrección adecuada a la percepción humana.
La unidad de intensidad luminosa es la candela (cd), una magnitud fundamental en el SI (Sistema Internacional de Unidades de Medida [2] ). Es la intensidad luminosa en una dirección dada, de una fuente de radiación monocromática de 555 nm (un tono de amarillo de 540 x 1012 Hz) cuya intensidad radiante es 1/683 Watt/estereorradián en dicha dirección. También puede ser expresada en relación con el flujo luminoso:
candela = lumen / estereoradián
Como puede verse, la relación entre la intensidad radiante y la intensidad luminosa para la luz de 555 nm es que 1 W/sr = 683 cd, aunque esta relación no se mantiene igual para el resto de frecuencias del espectro.
Nota: al estudiar el color (especialmente en informática o artes gráficas) se utilizan fuentes de radiación planas (monitores o lienzos), y aunque es una unidad fundamental, la intensidad luminosa no es adecuada para describir la radiación de fuentes muy pequeñas como los píxeles, sobre todo cuando están rodeados de muchos otros similares, por lo que es más útil utilizar el flujo luminoso en tales estudios.
§2.3 Densidad luminosa
La densidad de radiación
![]() afectada por el coeficiente de
iluminación relativa es la densidad luminosa. Su unidad es el Lux (lx),
definido como 1 lúmen/m2, o lo que es lo mismo: 1 candela · sr / m2.
Esta magnitud recibe otros nombres: iluminación (densidad luminosa incidente), iluminancia y radiancia
(densidad luminosa emitida). Es la proporcionada por los instrumentos de medición de luz utilizados en
fotografía (fotómetros).
afectada por el coeficiente de
iluminación relativa es la densidad luminosa. Su unidad es el Lux (lx),
definido como 1 lúmen/m2, o lo que es lo mismo: 1 candela · sr / m2.
Esta magnitud recibe otros nombres: iluminación (densidad luminosa incidente), iluminancia y radiancia
(densidad luminosa emitida). Es la proporcionada por los instrumentos de medición de luz utilizados en
fotografía (fotómetros).
La densidad luminosa es la que conocemos vulgarmente como "iluminación". En este sentido decimos que un sitio está bien o mal iluminado según sea su densidad luminosa. A título comparativo, la tabla adjunta muestra algunos valores típicos de densidad luminosa:
| Fuente de luminación | densidad luminosa lx |
| Máximo de luz solar | 100.000 |
| Día nublado | 10.000 |
| Luz de plenilunio | 0,2 |
| Luz de las estrellas | 0,0003 |
§2.4 Luminancia
La luminancia, luminosidad o brillo [7], es la intensidad luminosa
![]() por unidad de superficie, se designa por Y, y su unidad es el Nit (del latín "nittere"
- brillar-) definido como candela/m2. Es lo que coloquialmente designamos como "brillo"
de una pantalla o imagen. Corresponde a lo que la CIE define como luminosidad o claridad ("Lightness"),
definida por esta como un atributo de la sensación visual por el que un área parece que emite más o menos luz (todos tenemos
claro el concepto de lo que significa una estrella más o menos brillante).
por unidad de superficie, se designa por Y, y su unidad es el Nit (del latín "nittere"
- brillar-) definido como candela/m2. Es lo que coloquialmente designamos como "brillo"
de una pantalla o imagen. Corresponde a lo que la CIE define como luminosidad o claridad ("Lightness"),
definida por esta como un atributo de la sensación visual por el que un área parece que emite más o menos luz (todos tenemos
claro el concepto de lo que significa una estrella más o menos brillante).
Un aspecto curioso es que la respuesta del ojo humano a las variaciones de luminancia es prácticamente logarítmica. Basta una reducción del 18% de la luminancia entre dos objetos para que la luminancia de uno parezca la mitad de otro. A título orientativo se muestran los valores de luminancia para algunas fuentes de luz.
| Luminancia (nits) | Fuente |
| 1.6 * 109 | Disco solar a medio día |
| 600.000 | Disco solar en el ocaso |
| 120.000 | Lámpara incandescencia 60 W |
| 11.000 | Fluorescente |
| 8.000 | Cielo despejado |
| 2.500 | Disco lunar en plenilunio |
| 2.000 | Cielo cubierto. |
| 200 | Pantalla de ordenador |
| 0,0004 | Cielo en noche oscura |
Nota: los valores de brillo de las pantallas estándar son del orden de 150 a 250 nits. Tradicionalmente las pantallas planas tenían una menor luminancia que las de tubo CRT, pero actualmente (2004) alcanzan niveles e 400 nits.
Es frecuente establecer la luminancia como un porcentaje de otra que se establece como referencia (de forma explícita o implícita), que se denomina blanco de referencia Yw ("White reference"). Por ejemplo, un monitor puede tener un blanco cuya luminosidad Yw sea 100 candelas/m2, una luminosidad Y = 1 se refiere a este valor, 0.5 a la mitad, etc.
Nota histórica: Como se ha indicado, la unidad fundamental de fotometría es la intensidad luminosa, y el primer patrón fue también de intensidad luminosa [5], la bujía patrón, correspondiente a la luminosidad de una bujía real de esperma (*) construida según ciertas normas. Evidentemente este patrón no resultaba permanente y había dificultad para reproducirlo, por lo que se sustituyó por lámparas de incandescencia con filamento de carbón que eran calibradas con una bujía de esperma. Finalmente, en 1948 el patrón fotométrico pasó a ser un patrón de brillo (luminancia), definido en función del brillo de un cuerpo negro a la temperatura de solidificación del platino. En consecuencia la unidad fundamental (candela) pasó a ser definida en función del nuevo patrón como la intensidad luminosa tal que el brillo de un cuerpo negro a la temperatura de solidificación del platino sea de 600.000 candelas/m2.
Esta aparentemente extraña definición, que equivale a la enunciada anteriormente, se realizó con intención de que resultase equivalente a la anterior basada en base al patrón bujía, pero mediciones posteriores demostraron que era ligeramente inferior.
* Sustancia grasa que se extrae de ciertas cavidades de la cabeza del cachalote.
§3 El cuerpo negro
Casi todos los libros de física o cualquier disciplina relacionada con la luz y el color hacen referencia al cuerpo negro. Vamos a intentar una somera explicación sobre el mismo porque es un concepto importante para entender estas cuestiones:
En general cuando un cuerpo recibe radiación electromagnética (por ejemplo luz), una parte de esta radiación es absorbida y otra reflejada [6]. La fracción reflejada se denomina coeficiente de reflexión (r) y la fracción absorbida coeficiente de absorción (a). Ambos coeficientes son números abstractos tales que a + r = 1. El balance energético se ha simbolizado en la figura 4, donde H representa la radiación recibida; r·H la fracción reflejada y a·H la fracción absorbida. El término He representa la energía irradiada por el cuerpo en función de su propia temperatura (esta radiación es independiente que de que reciba o no energía H del exterior).
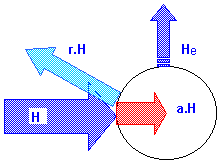
Fig 4 |
Nota: el inverso de r se denomina opacidad (1/r) y su logaritmo de base 10 (log 1/r) densidad. Por ejemplo, si una superficie refleja el 25% de la energía recibida, su coeficiente de reflexión es r = 0.25; su opacidad es 4 (1/0.25), y su densidad es 0.60 (log 4). Estas últimas magnitudes se utilizan principalmente en fotografía y artes gráficas.
La suma de energías reflejada y absorbida debe ser igual al total H de energía que incide sobre el
cuerpo: r·H + a·H = H --> (r + a) H = H -->
r + a = 1, pero observe que independientemente de esto, el cuerpo puede emitir cierta radiación por sí mismo
(señalada He en la figura). La energía reflejada no tiene efecto sobre el cuerpo, pero la absorbida y la
emitida tienen influencia en el equilibrio térmico.
Además de reflejar una parte de la radiación recibida, todos los cuerpos
emiten radiación He en razón de su propia temperatura (los seres humanos
emitimos radiación infrarroja). Cuando la energía
recibida es mayor que la emitida ( a · H > He ), el cuerpo se calienta; como consecuencia de éste
calentamiento la energía emitida aumenta. El proceso continúa hasta que se alcanza el equilibrio (ver a continuación
Temperatura del color ![]() ).
).
Un cuerpo cuyo coeficiente de reflexión fuese 1 (y el de absorción 0) sería
un espejo perfecto (reflejaría la totalidad de la energía recibida). Del
mismo modo, un cuerpo cuyo coeficiente de reflexión fuese 0 (y el de
absorción 1) sería un receptor perfecto (absorbería la totalidad de la
energía recibida). Por supuesto no existen cuerpos perfectamente
reflectantes ni perfectamente absorbentes, aunque pueden construirse espejos que reflejan más del 99% de la energía
recibida, y el negro de humo solo refleja el 1% de la energía que recibe.
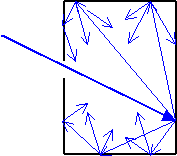
Fig. 5 |
Un receptor perfecto, que absorbe toda la energía incidente se denomina cuerpo negro. Es una abstracción teórica que no existe en la realidad, aunque puede ser simulado con bastante precisión por una pequeña abertura practicada en una caja que se ha pintado interiormente con negro de humo (fig 5). En este caso la abertura en sí misma es lo más parecido a un cuerpo negro.
No existe receptor más perfecto que el cuerpo negro, pero como veremos a continuación, tampoco existe radiador que lo supere, ya que las capacidades de absorción y radiación están en razón directa, por lo que es mejor denominarlo radiador perfecto.
Nota: no confundir el hecho de que el cuerpo negro no refleje nada de la energía recibida con el hecho de que pueda emitir él mismo energía si su temperatura es suficientemente elevada. En consecuencia un cuerpo negro puede no parecer negro desde el exterior. De hecho, la mayoría de aplicaciones del "cuerpo negro" en óptica se basan en la radiación emitida por él.
Si un cuerpo está en equilibrio térmico a una temperatura t
determinada, la energía absorbida es igual a la emitida ( a · H = He ). Esto exige que la energía recibida por
unidad de superficie en un tiempo dado sea igual a la emitida por unidad de superficie en el mismo tiempo.
Es decir: su poder emisivo y absorbente (
![]() ) deben ser iguales He
= Ha. Si recibe una densidad de radiación H del exterior, el balance de energías
por unidad de superficie comprende los siguientes factores:
) deben ser iguales He
= Ha. Si recibe una densidad de radiación H del exterior, el balance de energías
por unidad de superficie comprende los siguientes factores:
Densidad total recibida H
Densidad absorbida: Ha = a · H (poder absorbente)
Densidad reflejada: Hr = r · H
Densidad emitida: He (poder emisivo)
Puesto que Ha = a · H = He, puede establecerse que Ha / He = 1. La consecuencia es que la relación entre el poder absorbente y el emisivo de un cuerpo es constante e igual para todas las superficies a la misma temperatura (observe que en el supuesto no hemos mencionado para nada la naturaleza de la superficie). Este hecho se conoce como ley de Kirchoff, y tiene importantes repercusiones prácticas. Implica que si una superficie tiene un poder absorbente grande, su poder emisivo también lo es (en consecuencia el cuerpo negro es también el emisor perfecto). Recíprocamente, si una superficie tiene un poder absorbente pequeño, su poder emisivo también es pequeño. Esto explica, por ejemplo, que los termos se construyan con una superficie interior plateada (que tiene un gran poder reflexivo y un poder absorbente pequeño), porque su poder emisivo también es pequeño, y en consecuencia el termo perderá poca energía (calor) por radiación (la conducción por convección está limitada por las dobles paredes con un vacío interior) [1].
§4 Temperatura del color
Todos los cuerpos emiten radiación electromagnética de diversas longitudes de onda en función de su temperatura; es la denominada radiación térmica (el cuerpo humano la emite en la zona del infrarrojo 10-4 a 10-6 m). Cuando la temperatura es suficientemente elevada esta radiación corresponde al espectro visible y es conocido de antiguo que las substancias emiten luz cuando se calientan. Es el principio que hace resplandecer la llama de una vela o el filamento de la lámpara de incandescencia. La distribución espectral de esta radiación es dependiente de la temperatura alcanzada por el objeto. Por ejemplo, los herreros saben que la temperatura del hierro al "rojo cereza" en la fragua es muy inferior a la del hierro al "rojo-blanco".
En física se sabe que la SPD
![]() de un radiador depende de su temperatura. Las temperaturas bajas proporcionan tonos
rojos y amarillos, mientras las elevadas proporcionan tonos azules.
Precisamente la diferencia del color de luz proporcionada por una vela, una
lámpara de incandescencia normal, o una lámpara de cuarzo, radica la distinta
temperatura de trabajo de su material emisor.
de un radiador depende de su temperatura. Las temperaturas bajas proporcionan tonos
rojos y amarillos, mientras las elevadas proporcionan tonos azules.
Precisamente la diferencia del color de luz proporcionada por una vela, una
lámpara de incandescencia normal, o una lámpara de cuarzo, radica la distinta
temperatura de trabajo de su material emisor.
Es frecuente caracterizar el tipo de luz proporcionado por una fuente luminosa por su temperatura de color, en referencia a la temperatura (en grados Kelvin) que tendría un radiador perfecto que proporcionase el mismo tipo de luz. A título de orientación la tabla adjunta muestra las temperaturas de color típicas de distintas fuentes luminosas.
| Temperatura de color | Fuente luminosa |
| 1.000 K | Luz de vela |
| 2.500 - 3.500 K | Lámpara incandescencia |
| 4.000 - 5.000 K | Fluorescentes "luz día" |
| 5.000 - 6.000 K | Flash electrónico |
| 6.000 - 7.000 K | Luz diurna día luminoso |
Aunque la temperatura del color puede ser un indicador aproximado del tipo de luz (distribución espectral)
proporcionado por una fuente luminosa, se trata de una aproximación grosera de la SPD, que
es siempre un indicador más exacto de esta magnitud.
§4.1 Balance de blanco
La temperatura de color de la iluminación es determinante en el color de los objetos iluminados, en consecuencia es muy importante en las artes gráficas y especialmente en fotografía. En artes gráficas la temperatura de color estándar para trabajar con colores es de 5.000 K (en esta notación no se utiliza el símbolo de grado). Por su parte los fotógrafos saben perfectamente que no todas las fuentes de iluminación tienen la misma temperatura de color. Por ejemplo, si van a iluminar con luz natural o flash (que tiene una temperatura de color alta), utilizan una película adaptada a este tipo de luz (denominada "luz día"). Mientras que si la iluminación a utilizar es de incandescencia (por ejemplo una escena de interior) deben utilizar película apropiada a una temperatura de color más baja (aproximadamente 3200 K); es la película denominada "luz artificial" en el argot. La razón de esta selección es que en caso contrario el resultado deja mucho que desear.
Los diversos tipos de película están fabricados de forma que compensen los colores dominantes de cada temperatura de color. En consecuencia utilizando la película adecuada, las escenas de exterior y las interiores aparecen igualmente correctas. En cambio, si se utiliza película luz día para fotografías de interior, aparecen con un dominante rojo muy acentuado. Si por el contrario se utiliza película de luz artificial para fotografías al aire libre, aparecen excesivamente azules.
Como se ha señalado, la fotografía tradicional (que utiliza película sensible) tiene en cuenta la temperatura de color de la luz ambiente mediante una correcta selección de la película, y adicionalmente en el proceso de positivado. En la fotografía digital es posible tener en cuenta este factor mediante el denominado balance de blanco. Consiste en indicar a la cámara qué color es exactamente blanco, para que la propia cámara pueda realizar las correcciones oportunas de forma que efectivamente aparezca como tal, con independencia de la temperatura de color de la luz ambiente (simultáneamente se realizan las correcciones correspondientes a todos los colores).
El procedimiento utilizado consiste enfocar un blanco patrón (una tarjeta blanca) que cubra totalmente la escena y presionar algún botón. Alternativamente puede disponerse de un capuchón blanco traslúcido con el que se cubre el objetivo mientras se presiona el botón. Para evitar este inconveniente y no tener que realizar el calibrado cada vez que se obtiene una instantánea, algunas cámaras disponen de balances de blanco preconfigurados que corresponden a las temperaturas de color de las situaciones más frecuentes. Por ejemplo, incandescencia, fluorescencia, luz del sol y nublado. En estos casos basta seleccionar el tipo de iluminación actual y la cámara realiza el ajuste automáticamente.
Nota: además de las cámaras digitales, otros dispositivos de reproducción
(impresoras y pantallas) pueden requerir un ajuste de blanco. Por ejemplo, en las pantallas se utilizan los ajustes
de brillo y contraste para conseguir que un objeto blanco aparezca como realmente blanco
(![]() 9.5).
9.5).
[1] Las formas de transmisión de energía son tres: radiación, conducción y convección (esta última se presenta solo en líquidos y gases).
[2] El Sistema Internacional de Unidades de medida (SI) es un refinamiento del primitivo sistema MKS que utiliza 6 unidades básicas: metro, Kilogramo, segundo, amperio, grado Kelvin y candela.
[3] Estereoradián (sr) es el ángulo sólido que teniendo su vértice en el centro de una esfera de radio R, intercepta sobre la superficie de dicha esfera un área de valor R2 (equivalente a la de un cuadrado de lado R).
[4] En realidad los experimentos se realizaron en condiciones de luminosidad alta y de luminosidad atenuada. Los resultados mostraron que la sensibilidad aumenta mucho cuando la iluminación es muy atenuada (por ejemplo bajo la luz de las estrellas) y que bajo estas condiciones la sensibilidad máxima se desplaza ligeramente hacia las longitudes de onda mas bajas (hacia el rojo). Este efecto es conocido como efecto Purkinje.
[5] No confundir el patrón de medida con la unidad fundamental. El primero es una magnitud que pueda ser fácilmente reproducida y estable. Por ejemplo la distancia, medida a cierta temperatura, entre dos marcas en un bloque de platino que se conserva en cierto sitio. La unidad fundamental es aquella que se toma como base y a partir de la cual pueden expresarse las otras magnitudes físicas. Como su valor no puede ser completamente establecido en función de otras unidades, en su definición interviene necesariamente un patrón al menos. La elección de qué magnitud se considera fundamental y cual derivada puede ser algo arbitraria.
[6] La partes reflejada y absorbida no mantienen la misma proporción para todas las frecuencias recibidas, unas son absorbidas casi completamente mientras que otras son casi completamente reflejadas. Esta reflexión selectiva es precisamente el origen del "Color" que presentan los cuerpos fríos iluminados bajo luz blanca. En ocasiones, además de la reflexión normal, la superficie emite espontáneamente una radiación de longitud de onda algo mayor que la absorbida. El fenómeno se conoce como fluorescencia, y es especialmente notorio con luz ultravioleta (todos recordarán los extraños efectos de color que origina la "luz negra" en las discotecas).
[7] El brillo ("Brightness") es uno de los mejores ejemplos de la poca consistencia del vocabulario utilizado en este área. Desafortunadamente, además del enunciado se utiliza con otros significados: