Física de sonido

10.1 Generalidades, física del sonido

§1 Presentación

En este capítulo se exponen algunas ideas sobre el sonido en el ordenador; comenzando por algunos conceptos básicos sobre física del sonido, que consideramos un soporte mínimo e indispensable que ayude a comprender aspectos más técnicos de la relación de la informática con el fascinante mundo de la música y el sonido.

Los aspectos más concretos de la tecnología del sonido en el ordenador actual se han dejado deliberadamente en el aire, apenas apuntados; las razones son varias. En primer lugar el propio desconocimiento del autor (nunca me han interesado demasiado los aspectos tecnológicos de este tipo). En segundo lugar, el fulgurante desarrollo de la tecnología del hardware, hace que dispositivos punteros de hoy parezcan anticuados pasado mañana, por lo que nos parecen más importante las ideas básicas, mucho más perdurables, que los últimos diseños, marca, modelo o tecnología de tal o cual tarjeta de sonido. En tercer lugar, la descripción detallada de dispositivos concretos se saldría totalmente del enfoque que pretendemos para esta obra.

Este capítulo pretende ser simplemente una introducción al tema; introducción que puede servir como punto de partida para que los lectores más interesados puedan comenzar a buscar por sí mismos.

§2 Sinopsis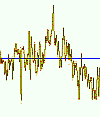

Según el Diccionario de la Lengua de la Real Academia Española, sonido es la sensación producida en el órgano del oído por el movimiento vibratorio de los cuerpos, transmitido por un medio elástico, como el aire. Luego nos aclara que es el efecto de la propagación de las ondas producidas por cambios de densidad y presión en los medios materiales, y en especial el que es audible.

A efectos prácticos podemos destacar dos ideas importantes: Que es una "sensación", (como la luz), por tanto subjetiva, y que el medio de propagación generalmente es el aire. Pero como el diccionario no es el mejor sitio para aprender física, añadiremos algunas puntualizaciones al respecto.

Suponiendo un medio aéreo (el normal para los seres humanos), el sonido está originado por cualquier perturbación en la presión atmosférica. Esta oscilación en más y en menos alrededor del valor normal, se propaga por el aire en lo que denominamos una onda acústica. En contra de lo que ocurre con las ondas electromagnéticas (la luz), cuya velocidad de propagación es una constante universal, la velocidad de propagación de las ondas acústicas depende en gran medida de las características del medio en que se transmiten. En las películas hemos visto como pegando el oído a la vía del tren se percibe más claramente, y antes, su llegada que si esperamos a oírlo por el aire [1]. También en el agua se propagan los sonidos mejor que en el aire; de esta circunstancia sacan provecho algunos animales marinos para su comunicación. Otra diferencia importante con respecto a la radiación electromagnética, es que las ondas acústicas necesitan de un medio elástico para su propagación, no pueden transmitirse en el vacío como aquellas.

Nota: En ciertos aspectos, el sonido y la luz comparten características comunes, por lo que frecuentemente estableceremos paralelismos y analogías entre ellos. El punto crucial, y común, es que ambos se refieren a la "percepción" en nuestra mente de fenómenos físicos, con todo lo que ello tiene de subjetivo, ya que la percepción humana es subjetiva (distinta para cada individuo). No es desde luego fácilmente cuantificable, ni sigue una relación de tipo lineal respecto al fenómeno que las origina. Otro punto importante es que estos fenómenos pueden ser estudiados desde un punto de vista físico (objetivo) e independiente de la percepción que el humano pueda tener de los mismos.

§3 El sonido en el aire

Los fenómenos que percibimos como sonido son vibraciones, y desde el punto de vista físico es equivalente considerarlas como desplazamientos oscilatorios (en dos direcciones opuestas) de las moléculas del aire, o como alteraciones de presión también oscilatorias [6]. Estas alteraciones inciden sobre el tímpano, y a través de los huesos del oído medio, son conducidas al oído interno, donde producen alteraciones electo-químicas que llegan hasta el cerebro por los nervios auditivos.

Hemos señalado que las alteraciones de presión que constituyen el sonido se desplazan a una velocidad que depende del medio; es lo que se conoce como velocidad de propagación. En el caso del aire a nivel del mar, esta velocidad es aproximadamente de 340 metros por segundo; es denominada Mach 1 en aviación [9].

De forma similar a lo que ocurre con la radiación electromagnética, el oído humano es capaz de percibir las perturbaciones de presión de las ondas acústicas. Aquí hay dos aspectos importantes a considerar: Uno es relativo a las frecuencias perceptibles; el otro a la energía necesaria para que la onda sea perceptible.

Nos referiremos a los aspectos energéticos más adelante (Intensidad Sonora ). Respecto al primer punto, el oído es sensible a una gama de frecuencias, el denominado rango de frecuencias audibles o frecuencias de "Audio". Generalmente se acepta que comprende entre 20 Hz y 20,000 Hz, aunque existen componentes armónicos () de audio que se extienden muy por encima de los 20 KHz. También aquí, algunos animales son capaces de percibir y utilizar, sonidos fuera del rango que es perceptible a los humanos. Por ejemplo, perros, gatos, delfines y murciélagos.

El sistema de altavoces y los auriculares que suelo conectar en el ordenador de trabajo, son de calidad mediana. El primero es un sistema auto-amplificado de 2 altavoces y 9 W por canal que, de acuerdo con sus especificaciones, tiene un rango de respuesta de 120 Hz a 20 KHz. El de los auriculares es de 18 Hz a 22 KHz. Como puede verse, es más fácil hacer que la membrana de estos últimos funcionen a altas y bajas frecuencias, que la de los altavoces, que por ser mayores tienen mayor inercia.

§3.1 Amplitud, tono y timbre

Como ocurre con todos los fenómenos ondulatorios, en el sonido son importantes dos parámetros: La frecuencia y la amplitud. La frecuencia es percibida como tono, las frecuencias elevadas se perciben como tonos agudos, las más bajas como tonos graves. Por su parte, la amplitud se percibe como intensidad, volumen o sonoridad. Las vibraciones de gran amplitud se perciben como sonidos fuertes, las de pequeña amplitud son sonidos débiles.

La frecuencia F de un sonido y su longitud de onda L están directamente relacionadas con la velocidad de propagación V en la forma:

L = V / F <===> F = V / L

Por ejemplo, a una frecuencia de 10 KHz le corresponde una longitud de onda:

L = 340 / 10 · 10³ m = 34 mm

Las longitudes de onda de las frecuencias audibles oscilan entre 1.7 cm y 17 metros. Los murciélagos pueden utilizan sonidos de unos 10 KHz. Los 34 mm de longitud de onda de este "Sonar" es suficiente para discriminar y capturar insectos en vuelo [8].

El conocimiento de la longitud de onda del sonido es fundamental cuando se trabaja en espacios acústicos como estudios de grabación, micrófonos, cajas acústicas, etc. Cuando se trata del sonido, además de la frecuencia (tono) y amplitud (sonoridad) también es importante el timbre o calidad del tono. Siguiendo nuestro paralelismo con la radiación electromagnética, de la que no existen luces de color puro, en la vida real tampoco no existen sonidos puros (de una sola frecuencia). Los sonidos reales son compuestos de vibraciones de muchas frecuencias, precisamente la proporción de las frecuencias componentes es lo que caracteriza el timbre de los sonidos, desde la voz humana a los instrumentos musicales.

Incluso un sonido más o menos puro como una nota de piano, tiene una componente fundamental, que corresponde a la frecuencia de la propia nota, pero está acompañada de toda una gama de frecuencias (múltiplos y divisores) por arriba y por debajo de esta frecuencia fundamental. Son los denominados componentes armónicos, que en conjunto caracterizan la nota. Por ejemplo, la nota más baja del piano es de 27 Hz y la más alta de unos 4 KHz. El LA central (natural) -nota A en la nomenclatura anglosajona- es de 440 Hz, sin embargo está acompañado de componentes armónicos de 220, 110, 55, ..., 880, 1320, 1760, Etc. que exceden con mucho las frecuencias fundamentales de las teclas extremas. Considere que son precisamente las amplitudes de los armónicos, lo que permiten distinguir un LA natural de piano de un LA de saxo o de clarinete.

Fig. 1

Otro aspecto importante para la identificación de sonidos es su evolución en el tiempo. La amplitud del sonido tiene una evolución desde el momento inicial hasta que desaparece, y esta evolución concierne tanto a la componente fundamental como a sus armónicos. Su representación es la envolvente del sonido y tiene cuatro partes características: El ataque ("Attack") es la fase en que el sonido va creciendo en intensidad hasta alcanzar un máximo. El sostenido ("Sustain") es una fase en que la intensidad es más o menos constante; en ocasiones después de un pequeño descenso ("Decay") después de la amplitud máxima. Finalmente, la desaparición ("Release") es la fase en que la intensidad va disminuyendo hasta desaparecer. Por ejemplo, una palmada tiene un tiempo de ataque de unos 2.5 ms en los que la amplitud crece muy rápidamente; un sostenimiento de unos 3 ms y desaparece en otros 2.5 ms. En cambio, el tiempo de ataque de un gong es mucho más lento, del orden de 1 s; su sostenimiento es de 1.5 s y su desaparición del orden de 30 segundos o más. Tenga en cuenta que la intensidad de los armónicos (su envolvente) no evoluciona igual que la de la frecuencia principal y es a su vez distinta para los distintos instrumentos.

Nota: Generalmente los armónicos de alta frecuencia se atenúan antes que los de frecuencias bajas, que son más persistentes.

La figura 1 muestra una imagen simplificada (utilizando trazos rectos) de la envolvente de un sonido. Es una representación conocida como modelo ADSR ("Attack-Decay-Sustain-Release"), que es utilizada en ciertas técnicas de síntesis que utilizan tablas de ondas [7].

Puesto que el sonido es la percepción de vibraciones mecánicas en un medio elástico (el aire), estas vibraciones pueden ser medidas en término de variaciones ± del valor de la presión atmosférica, cuyo valor máximo puede ser expresado por:

p_max = A B 2 π/ L = A B k

En esta fórmula, A es la amplitud de la vibración; B es el módulo de elasticidad de volumen, o módulo volumétrico ("Bulk modulus"), del medio de propagación (aire en nuestro caso); L es la longitud de onda y π es el número Pi (3.1415...). El término k (2 π / L) es conocido como número de onda o constante de propagación.

§4 Magnitudes físicas

Desde el punto de vista de la física existen dos magnitudes que tienen importancia en la percepción del sonido: La potencia y la intensidad sonoras.

§4.1 Potencia Sonora

El frente de ondas que se propaga alrededor de un punto transporta cierta energía [2]. Esta energía es captada por el tímpano, y es precisamente la responsable de que podamos oírlo. Es bastante intuitivo que cuanto más extenso sea este frente (más alejado del punto inicial) la energía estará menos concentrada (el sonido se percibe como más débil). Por esta razón la energía en sí misma no es muy representativa de lo "Fuerte" que puede resultar un sonido. Como veremos a continuación, es más representativa la energía por unidad de superficie. Sin embargo, indicaremos aquí que el oído es un órgano extraordinariamente sensible en este aspecto, pudiendo percibir energías infinitesimales. Se estima que al hablar en tono normal desarrollamos una una potencia de 0.00001 W (10^-5 W), y tres veces este valor para un grito [3].

§4.2 Intensidad sonora

La intensidad I de un sonido puede medirse mediante la energía que transporta por unidad de superficie (medida en perpendicular a la dirección de propagación); se expresa en W/m². Esta magnitud que depende de la amplitud y frecuencia de la fuente sonora, y es independiente de cualquier consideración subjetiva (del observador).

Se acepta que la intensidad del sonido más tenue perceptible por el oído humano normal es de 10^-12 W/m², y que 1 W/m² es el umbral del dolor. En base a estos datos, puede afirmarse que el oído humano es realmente notable y que su rango de percepción es increíble (podemos suponer como es el de algunos animales). El físico Alexander Wood lo comparó con la variación de luminosidad aparente de una lámpara de 50 Watt encendida en Londres para una persona que partiese de su proximidad y se alejase paulatinamente hasta Nueva York. Precisamente este enorme rango de intensidades sonoras perceptibles por el oído ha motivado que, como veremos en el próximo epígrafe, se utilice para su medición no una escala lineal, sino logarítmica.

Suponiendo que la energía se distribuye uniformemente alrededor del que habla, un interlocutor a 1 m percibe una intensidad I = 10^-5/ (4 π 1²) = 79.577 10^-8 W/m². Si en un teatro queremos conseguir que a 20 m del escenario percibamos la conversación de dos actores como si estuviésemos en la propia escena, debemos utilizar un amplificador que proporcione una potencia sonora Ps:

Ps / (4 π 20²) = 10^-5/ (4 π 1²) ==> Ps = 10^-5(4 π 20²) / (4 π) = 4 mW. [5]

§4.3 Nivel de presión acústica

Otra forma de referirse a la energía transportada por un sonido es su nivel de presión SPL ("Sound Pressure Level") o volumen acústico, que depende de la amplitud de la vibración. Es importante significar que la misma frecuencia nos parece de tono distinto cuando cambia su intensidad [4] y que niveles elevados se consideran dañinos para la salud y pueden llegar a producir sensaciones dolorosas.

El volumen acústico se mide en Bels, abreviadamente B, nombre elegido en honor de Alexander Graham Bell. Tiene su origen en los laboratorios Bell de AT&T cuando necesitaban un método para medir las pérdidas de señal en líneas telefónicas. El volumen acústico ß de un sonido de intensidad I expresado en Bels se define como:

              I

ß = log -----    (Bels)

               I_o

Como la unidad resultaba demasiado grande, se utiliza el decibelio(décima parte del Bel) designado dB que ha quedado como unidad "de facto" para la medida del volumen acústico. Así pues, el volumen acústico ß de un sonido de intensidad I expresado en decibles se define como:

                     I

ß = 10 log -----    (dB)

                     I_o

Como puede verse, se trata de un cociente entre dos magnitudes, expresado en una escala logarítmica. Salvo indicación en contrario, el valor de referencia I_o es 10^-12 W/m² (intensidad del sonido más tenue perceptible por el oído humano), que se considera como punto origen para las medidas acústicas. De la propia definición se deduce que el volumen acústico correspondiente a I_o es:

I_o

ß = 10 log ----- = 10 log 1 = 0

I_o

La intensidad de 1 W/m² (umbral del dolor), equivalente a una presión sonora de 120 dB, y 1 dB es la mínima variación de intensidad de un sonido que puede detectar el oído. De la aplicación de la fórmula se deduce que duplicar la intensidad de un sonido (pasar de un valor I₁ a otro 2 · I₁) supone una variación de 10 log 2 = 3.01 dB.

Nota: observe que la intensidad I de un sonido es una magnitud absoluta, independiente del observador, mientras que el nivel de presión sonora SPL, es un valor relativo que toma como referencia un nivel de señal relacionado con un observador humano estándar. La ventaja de utilizar la presión acústica SPL en dB frente a la intensidad, es que al estar referida al nivel de percepción humano, es más significativa para hacernos una idea de "cuanto" de fuerte es percibido un sonido. Además, tratándose de sonidos para "consumo" humano, voz, música, señales acústicas, Etc. el rango a manejar es de 120 en vez de 1.000.000.000.000. Por ejemplo, la diferencia entre dos intensidades de 10^-8 W/m2 y 10^-4 W/m2, que son 10,000 W/m2, puede ser expresado como una diferencia de 40 decibelios (4 Bels).

Las medidas en Bels y decibels representan un cociente entre dos valores. Es decir, una medida relativa como lo podría ser el % (ver a continuación), que no tiene sentido si no se conoce el valor de referencia. Es frecuente encontrar esta medida en todo tipo de trabajos que tienen que ver con el sonido, y no siempre el valor de referencia se refiere a 10^-12 W/m². Por ejemplo, al referirse a amplificaciones o atenuaciones de señales eléctricas, se utiliza como valor de referencia el valor de la señal (tensión) de entrada, que es equivalente, ya que las potencias de las señales eléctricas son proporcionales al cuadrado de su tensión.

W = V . I

I = V / R

W = V²/R §4.3a

Significado: W = potencia; I = intensidad; R = resistencia.

Así pues, si una señal eléctrica sufre una amplificación o atenuación, pasando de V_o a V en un dispositivo, la ganancia (o pérdida) puede ser expresada también en decibelios en función de las tensiones y resistencias de entrada y salida:

§4.3b

x dB = 10

V²/R

log --------- = 20

V_o²/R_o

V Ro

log ---------- = 20

V_o R

Log --- + 20

Log ---- = 20

Log --- + K

Como puede verse, cuando se utilizan estas expresiones en dispositivos amplificadores, es necesario indicar las resistencias de salida y entrada. Caso de ser iguales (Ro = R) la expresión K vale cero, de forma que la amplificación solo depende del logaritmo del cociente de las tensiones de entrada y salida.

Nota: Los modernos sistemas de audio tienen una impedancia de salida relativamente baja, mientras que es alta la de entrada. En consecuencia existe un mínimo intercambio de energía entre ambos lados. En estas condiciones el cociente Ro/R es un valor alto.

En realidad es raro encontrar expresiones de % en trabajos de acústica, aunque a veces se utiliza. La expresión para convertir entre ambas es:

Ganancia	Variación de señal en %
+ 12 dB + 6 dB ± 0 dB - 6 dB - 12 dB - 20 dB - 40 dB - 60 dB - 80 dB	400 % 20 log (400/100) 200 % 20 log (200/100) 100 % 20 log (1) 50 % 20 log (50/100) 25 % 20 log (25/100) 10 % 20 log (10/100) 1 % 20 log (1/100) 0.1 % 20 log (0.001) 0.01 % 20 log (0.0001)

y %

x dB = 20 log --------

100

En el cuadro se muestran algunos ejemplos de las variaciones de señal conseguidas con un amplificador en función de los ajustes en el control de ganacia (dB). Observe que cuando la ganancia es cero, la señal de salida coincide con la de entrada.

Como resultado de las distintas magnitudes que pueden relacionarse en las medidas acústicas, es frecuente encontrar las siguientes expresiones:

dB Fs decibelios relativos a "Full Scale". Es la más utilizada en trabajos de audio. Como valor de referencia se utiliza el máximo que puede alcanzar la señal [10] (se suponen tensiones). En consecuencia los resultados son negativos (los cocientes son siempre menores que la unidad). En las señales digitales este valor viene determinado por la profundidad de muestreo ( 10.2), que para los sistemas de sonido del PC son 8 o 16 bits, por lo que el denominador (señal "full scale") puede adoptar los valores máximos 255 y 65535. Poniendo estos valores en el denominador y 1 en el numerador (valor mínimo de la señal distinto de cero) en la fórmula §4.3b , los rangos para estas señales son de 0 a -48 dB para 8 bits y 0 a 0 a -96 dB. para 16 bits.
dB r decibelios relativos a una referencia absoluta. Se utiliza en mediciones de precisión y se indica siempre el valor r utilizado como referencia.
dB V decibelios relativos a 1 Voltio. En este caso el divisor es 1 y la expresión §4.3b se reduce a dB = 20 log V + K
dB m decibelios relativos a 1 mW. Suele utilizarse en radiodifusión. Cuando se utiliza en mediciones acústicas debe indicarse la resistencia, ya que en audio, el rendimiento y eficacia de los equipos se expresan en voltajes en lugar de potencias. Teniendo en cuenta que los equipos profesionales de audio suelen tener una impedancia de entrada entre 600 y 150 Ohmios. 1mW representa tensiones entre 0.7746 y 0.3873 Voltios (fórmula §4.3a ).
dB u decibelios utilizando una referencia de voltaje de 0.7746 V. O lo que es lo mismo, utilizando una potencia de referencia de 1 mW (dB m) y una resistencia de referencia de 600 Ohms.
dB spl decibelios "Sound Pressure Level". En las medidas acústicas es frecuente utilizar una intensidad de referencia de 0.1 W/m².

Bibliografía:

"Personal Computer Audio Quality Measurements" Dr. Steven Harris & Clif Sanchez

§5 Sensibilidad humana

Como hemos señalado, el oído humano es un instrumento registrador extremadamente sensible; es capaz de percibir vibraciones del aire del orden de 10^-11 m, aunque evidentemente esta sensibilidad no es la misma para todos los individuos ni para todas las frecuencias. Fletcher y Munson (F&M) fueron los primeros investigadores que en los años 30 establecieron la sensibilidad humana a sonidos de diversa amplitud y frecuencia, demostrando que la sensibilidad del oído es extremadamente dependiente de la frecuencia, registrando una sensibilidad máxima entre 3 y 4 KHz. Por encima y debajo de estas frecuencias los sonidos se perciben más débilmente.

Según estos resultados resulta evidente que conocer el SPL de un sonido no proporciona suficiente información sobre su sonoridad ("cuanto" de fuerte lo percibimos); habría que indicar su frecuencia y conocer el grado de sensibilidad a esta última.

Con objeto de dar una medida lo más fiel posible de la "sonoridad" de un sonido, Fletcher y Munson establecieron una medida para la sonoridad y una serie de curvas de igual sonoridad para varios niveles de presión acústica, desde el umbral de audición (0 dB), a niveles dañinos para la salud (120 dB), en intervalos de 10 dB.

Observe que utilizamos el término sonoridad para describir el nivel de sensación que produce un sonido. La unidad de sonoridad phon, es la que corresponde a un sonido de 1000 Hz expresado en dB.

Para determinar la sonoridad de una nota de cualquier frecuencia F, se determina el SPL en dB de un sonido de 1000 Hz que proporcione la misma sensación de volumen sonoro.

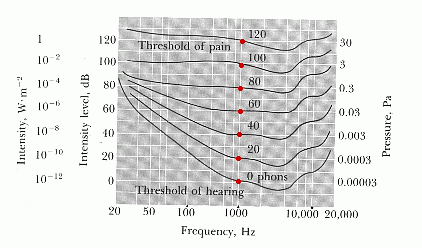
En la figura adjunta se muestran una serie de estas curvas de F&M. En abcisas se muestran (en escala logarítmica) las frecuencias F de 20 a 20,000 Hz (audibles); en ordenadas se muestran las intensidades I del sonido en W/m²; en decibelios, y la presión máxima Pa correspondiente en pascales (Newton/m²).

Las curvas muestran puntos de igual sonoridad, la inferior corresponde al umbral de percepción, la superior al umbral de dolor. Por ejemplo, un sonido de 100 Hz a 52 dB y otro de 10 KHz a 52 dB tienen la misma sonoridad que una nota de 1 KHz a 40 dB, lo que significa que los tres tienen una sonoridad de 40 fones.

Nota: El valor de la presión acústica, expresada en decibelios, ponderada en función de la frecuencia, se conoce como "A-weighted", y se indica añadiendo una letra "A" a la medida. Por ejemplo: 15 dBA.

§6 Webografía

SweetWater http://www.sweetwater.com/insync/word.php

Glosario de términos relacionados con el sonido.

Handbook for Acoustic Ecology http://www.sfu.ca/sonic-studio/handbook/

Es la versión digital actualizada de un libro cuya primera edición vio la luz en 1978. Producto a su vez de un proyecto de investigación de la universidad canadiense Simon Frazer de Vancouver (Columbia Británica). Contiene información sobre infinidad de conceptos y términos relacionados con el sonido.

Inicio.

[1] Naturalmente eso lo hacen los "Indios" en las películas, pero es totalmente desaconsejable hacerlo en la realidad.

[2] La energía es la capacidad de producir un trabajo. A su vez el trabajo puede transformarse en movimiento mecánico o calor.

[3] La potencia es la energía dividida por el tiempo (energía en unidad de tiempo). Generalmente expresada en Vatios ("Watts"). 1 W = 1 Julio/s. = 0.10197 Kgm/s.

[4] Esta circunstancia debe ser tenida en cuenta cuando se mezclan sonidos; deben ser comprobados a diversos volúmenes acústicos. Como regla general, si una mezcla suena bien a un nivel bajo, sonará mejor a niveles más elevados.

[5] Naturalmente la potencia eléctrica debería ser muy superior; generalmente los altavoces son dispositivos que proporcionan un rendimiento muy pobre entre la energía eléctrica consumida y la energía acústica radiada. Además en estas consideraciones suponemos que la energía se reparte uniformemente alrededor de la fuente, cosa que casi nunca es cierta.

[6] Las sinusoides que representan los desplazamientos de las moléculas y las variaciones de presión, están desfasadas entre sí 1/4 de onda.

[7] En muchos instrumentos, la composición espectral (de armónicos) durante la ejecución de una nota, permanece aproximadamente constante durante el periodo de "Sustain". Esta circunstancia es aprovechada para guardar un trozo de esta forma de onda en una tabla ("Wavetable"). Posteriormente, la onda total es reconstruida repitiendo la muestra un número de veces adecuado hasta alcanzar la duración total deseada. Simultáneamente la amplitud es modulada de forma que se ajuste lo más posible a un patrón ADSR determinado.

[8] Se acepta que pueden percibir sonidos entre 1 y 80 KHz. Para el delfín entre 2 y 100 KHz

[9] La velocidad del sonido en el aire se mide generalmente en una "atmósfera estándar" (15.6ºC, 1013,25 mb/cm², 1,325 kg/m³) es aproximadamente 340.46 m/s. En agua dulce, a 30ºC, es de 1509.6 m/s, mientras que en la de mar, con la misma temperatura, con una concentración de sales de 35%, es de 1546.2 m/s. Se estima que cuando la temperatura aumenta en un grado centígrado, la velocidad del sonido lo hace en 2.5 m/s; si la salinidad se incrementa en 1%, la velocidad presentará un incremento 1.4 m/s; y si la presión sube 10 atmósferas (100 m. de profundidad), el incremento es de 1.8 m/s. En el acero (vías del tren) la velocidad de propagación es de unos 5100 m/s.

[10] Cuando la señal llega a los valores máximo o mínimo se dice que hay "saturación".

Inicio