2.2.4a Formas de representación binaria de las magnitudes numéricas
§1 Presentación de un problema
Antes de entrar en detalles, haremos un pequeño inciso para señalar el principal problema que entraña la representación de cantidades numéricas en los ordenadores digitales.
En el apartado dedicado al Ordenador digital (![]() 0.1) recordamos que la información está representada en forma digitalizada. Es decir, reducida a cantidades
discretas representadas por números y estos a su vez, expresados en formato binario. Como la serie de los números
reales tiene infinitos números (desde -Infinito a +Infinito [0]), es imposible su representación completa en
cualquier sistema de representación. Además, aunque un número puede contener una cantidad indefinida de cifras,
los bits destinados a almacenarlas son necesariamente limitados [3].
Como consecuencia, en la informática real solo es posible utilizar un
subconjunto finito del conjunto de los números reales.
0.1) recordamos que la información está representada en forma digitalizada. Es decir, reducida a cantidades
discretas representadas por números y estos a su vez, expresados en formato binario. Como la serie de los números
reales tiene infinitos números (desde -Infinito a +Infinito [0]), es imposible su representación completa en
cualquier sistema de representación. Además, aunque un número puede contener una cantidad indefinida de cifras,
los bits destinados a almacenarlas son necesariamente limitados [3].
Como consecuencia, en la informática real solo es posible utilizar un
subconjunto finito del conjunto de los números reales.
El rango y precisión (número de cifras) del subconjunto de números que pueden representarse en
una máquina dada, dependen de la arquitectura, y para el lenguaje C++, depende
además del compilador (![]() 2.2.4).
Puesto que existen ocasiones en que las aplicaciones informáticas
necesitan manejar números muy grandes y muy pequeños, se ha derrochado mucho ingenio para conseguir
representaciones binarias con la máxima precisión en el
mínimo espacio, y para que estos formatos puedan ser manipulados por implementaciones hardware
lo más simples posible. También ha sido necesario ingeniar artificios para detectar y prevenir situaciones en las que un
resultado se sale por arriba o por abajo del rango permitido, al tiempo que se
mantiene el máximo de precisión en los cálculos.
2.2.4).
Puesto que existen ocasiones en que las aplicaciones informáticas
necesitan manejar números muy grandes y muy pequeños, se ha derrochado mucho ingenio para conseguir
representaciones binarias con la máxima precisión en el
mínimo espacio, y para que estos formatos puedan ser manipulados por implementaciones hardware
lo más simples posible. También ha sido necesario ingeniar artificios para detectar y prevenir situaciones en las que un
resultado se sale por arriba o por abajo del rango permitido, al tiempo que se
mantiene el máximo de precisión en los cálculos.
Hay que recordar que, incluso manejando cantidades dentro del rango, pueden presentarse fácilmente situaciones con errores de bulto que serían catastróficas en determinadas circunstancias. Por ejemplo, en cálculos de ingeniería. Supongamos una situación en que el compilador C++ tiene que multiplicar una serie de cantidades definidas en la máxima precisión:
long double r = x * y * z;
y que el orden de ejecución x * y * z es en este caso de izquierda a derecha. Si en un momento dado los valores de x e y son suficientemente pequeños (próximos al límite inferior permitido para long double), el primer producto x * y puede resultar inferior al mínimo que puede representar el compilador, originándose un "underflow". El resultado intermedio sería cero, y su producto por z también cero, con independencia del valor de esta última variable (que suponemos grande). El valor cero del resultado r podría a su vez propagarse inadvertidamente a otros cálculos. Observe también, que si la operación hubiese sido programada en otro orden. Por ejemplo:
long double r = x * z * y;
Tal vez el error no hubiese llegado a presentarse, dando la sensación que el código es seguro con los mismos valores de las variables. No es necesario señalar que este tipo de errores pueden acarrear consecuencias desastrosas. Por ejemplo, en cálculos de ingeniería. Para que el lector pueda formarse visión más tangible del problema, le invito a visitar esta interesante página (en inglés) Some disasters attributable to bad numerical computing.
Otros tipos de errores de precisión son más insidiosos aún. Para comprobarlo pruebe el lector este sencillo programa:
#include <iostream.h>
int main (void) {
float f = 3.0/7.0; // M1:
if (f == 3.0/7.0)
cout << "Igual" << endl;
// M2:
else
cout << "Desigual" << endl;
return 0;
}
La salida, con el compilador Borland C++ 5.5 es
Desigual
La explicación es que aquí las constantes 3.0 y 7.0 han
sido consideradas como números de coma flotante de doble precisión (double),
y el resultado de 3.0/7.0, que es del mismo tipo, sufre una conversión
estrechante (![]() 4.9.9)
a float, con pérdida de precisión, antes de la asignación a f
en M1. El mismo valor 3.0/7.0 (double) es comparado en M2 con el
de f (float), con el resultado de que no son iguales.
4.9.9)
a float, con pérdida de precisión, antes de la asignación a f
en M1. El mismo valor 3.0/7.0 (double) es comparado en M2 con el
de f (float), con el resultado de que no son iguales.
La comprobación de las afirmaciones anteriores es muy sencilla: basta modificar la línea M1 del programa por alguna de estas dos:
double f = 3.0/7.0; // M1.1:
long double f = 3.0/7.0; // M1.2:
Después de la sustitución, en ambos casos la salida es
Igual.
Si deseamos mantener la variable f como un float, una posible solución sería cambiar la sentencia
M2 (intente encontrar la explicación por sí mismo en ![]() 3.2.3c):
3.2.3c):
if (f == 3.0f/7.0f) cout << "Igual" << endl; // M2.1:
En el apartado que dedicamos a las conversiones estándar (![]() 2.2.5), encontrará explicación del porqué no funcionaría ninguna de las versiones siguientes:
2.2.5), encontrará explicación del porqué no funcionaría ninguna de las versiones siguientes:
if (f == 3.0f/7.0) cout << "Igual" << endl; // M2.2:
if (f == 3.0/7.0f) cout << "Igual" << endl; // M2.3:
§2 Formas de representación binaria
La necesidad de representar no solo enteros naturales (positivos), sino también valores negativos e incluso fraccionarios (racionales), ha dado lugar a diversas formas de representación binaria de los números. En lo que respecta a los enteros, se utilizan principalmente cuatro:
Lo relativo a los fraccionarios se indica más adelante
![]() .
.
§2.1 Código binario sin signo:
Las cantidades se representan de izquierda a derecha (el bit más significativo a la izquierda y el menos significativo a la derecha) como en el sistema de representación decimal. Los bits se representan por ceros y unos; cero es ausencia de valor, uno es valor. Por ejemplo, la representación del decimal 33 es 100001.
Si utilizamos un octeto para representar números pequeños, y mantenemos la costumbre de separar las cifras en grupos de 4 para mejorar la legibilidad, su representación es: 0010 0001.
Con este sistema todos los bits están disponibles para representar una cantidad; por consiguiente, un octeto puede albergar números de rango
0 <= n <= 255
Nota: aunque la representación interna (en memoria) suele tener el bit más
significativo a la izquierda, el almacenamiento en dispositivos externos
(disco) no tiene que ser forzosamente igual. Existen casos en los que la
representación externa es justamente al contrario, el bit más significativo
a la derecha, lo que supone que estos bytes deben ser invertidos durante los
procesos de lectura/escritura. Existen casos en que una misma
aplicación sigue distintos criterios para la alineación del bit más
significativo según el tipo de dato que se escribe en el disco. Por
supuesto la situación se complica cuando el número está representado por
más de un octeto. En este caso también puede jugarse con el orden de
escritura de los octetos. Véase al respecto Orden
de Almacenamiento (![]() 2.2.6a)
2.2.6a)
§2.2 Código binario con signo
Ante la necesidad de tener que representar enteros negativos, se decidió reservar un bit para representar el signo. Es tradición destinar a este efecto el bit más significativo (izquierdo); este bit es 0 para valores positivos y 1 para los negativos. Por ejemplo, la representación de 33 y -33 sería:
+33
0010 0001
-33
1010 0001
Como en un octeto solo quedan siete bits para representar la cantidad, con este sistema un Byte puede representar números en el rango:
- 127 <= n <= 127
El sistema anterior se denomina código binario en magnitud y signo. Aparentemente es el primero y más
sencillo de los que se pueden discurrir, además de ser muy simple para
codificar y decodificar. Sin embargo, la circuitería electrónica necesaria
para implementar con ellos operaciones aritméticas es algo complicada, por lo
que se dispusieron otros sistemas que se revelaron más simples en este sentido.
§2.3 Código binario en complemento a uno
En este sistema los números
positivos se representan como en el sistema binario en magnitud y
signo, es decir, siguiendo el sistema tradicional, aunque reservando el bit más
significativo, que debe ser cero. Para los números negativos se utiliza el
complemento a uno, que consiste en tomar la representación del correspondiente número positivo
y cambiar los bits 0 por 1 y viceversa (el bit más significativo del número
positivo, que es cero, pasa ahora a ser 1). En capítulo dedicado a los Operadores de manejo de bits
(![]() 4.9.3),
veremos que C++ dispone de un operador específico para realizar estos complementos a uno.
4.9.3),
veremos que C++ dispone de un operador específico para realizar estos complementos a uno.
Como puede verse, en este sistema, el bit más significativo sigue representando el signo, y es siempre 1 para los números negativos. Por ejemplo, la representación de 33 y -33 sería:
+33
0010 0001
-33
1101 1110
§2.4 Código binario en complemento a dos:
En este sistema, los números positivos se representan como en el anterior, reservando también el bit más significativo (que debe ser cero) para el signo. Para los números negativos, se utiliza un sistema distinto, denominado complemento a dos, en el que se cambian los bits que serían 0 por 1 y viceversa, y al resultado se le suma uno.
Este sistema sigue reservando el bit más significativo para el signo, que sigue siendo 1 en los negativos. Por ejemplo, la representación de 33 y -33 sería:
+33
0010 0001
-33
1101 1110 + 0000 0001
1101 1111
El hardware necesario para implementar operaciones aritméticas con números representados de este modo es mucho más sencillo
que el del complemento a uno, por lo que es el sistema más ampliamente utilizado [8]. Precisamente esta forma
de representación interna es la respuesta al problema presentado en la página
adjunta (![]() Problema)
Problema)
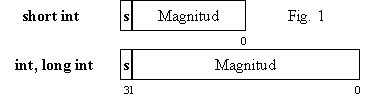 Nota: el manual Borland C++ informa que los tipos enteros con signo, tanto los
que utilizan dos octetos (16 bits) como los que utilizan una palabra de 4
Bytes (32 bits), se representan internamente en forma de código binario en complemento a dos (Fig. 1).
Nota: el manual Borland C++ informa que los tipos enteros con signo, tanto los
que utilizan dos octetos (16 bits) como los que utilizan una palabra de 4
Bytes (32 bits), se representan internamente en forma de código binario en complemento a dos (Fig. 1).
Precisamente los procesadores Intel 8088, sus descendientes y compatibles, almacenan internamente los números en
esta forma, y para facilitar la rápida identificación del signo, disponen de
un bit (SF) en el registro de estado (![]() H3.2) que indica si el
resultado de una operación tiene a 1 o a
0 el bit más significativo.
H3.2) que indica si el
resultado de una operación tiene a 1 o a
0 el bit más significativo.
§3 Números fraccionarios
A continuación exponemos brevemente los detalles del formato utilizado para representación interna de los números fraccionarios. Es decir, cómo son representados en forma binaria los números con decimales.
§3.1 Notación científica
En ciencias puras y aplicadas, es frecuente tener que utilizar números muy grandes y muy pequeños. Para facilitar su representación, se desarrolló la denominada notación científica (también denominada engineering notation en la literatura inglesa) en la que el número es representado mediante dos cantidades, la mantisa y la característica, separadas por la letra E/e.
Nota: en esta notación las letras E/e no tienen nada que ver con la constante e (2.71828182...) base de los logaritmos Neperianos. Es meramente un símbolo para separar dos partes de una expresión (podría haberse utilizado cualquier otro).
La mantisa es la parte significativa del número (las cifras significativas que se conocen [5] ). La característica es un número entero con signo, que indica el número de posiciones que hay que desplazar a la derecha o a la izquierda el punto decimal (explícito o implícito). Por la razón señalada (que la característica indica la posición del punto decimal), esta representación es también conocida como de "punto flotante".
La característica puede ser interpretada también como la potencia de 10 por la que hay que multiplicar la mantisa para obtener el número. Es decir: si V es el número, m la mantisa, y c la característica, resulta: V = m . 10c. Esta notación (matemática tradicional) es equivalente a V = mec = mEc en notación científica
Ejemplos:
Expresión Valor
23.45e6 23.45 10^6 == 23450000
-2e-5 -2.0 10^-5 == -0.00002
3E+10 3.0 10^10 == 30000000000
-.09E34 -0.09 10^34 == -900000000000000000000000000000000
§3.1.1 Notación normalizada
Puede verse que la notación científica permite varias formas para un mismo número. Por ejemplo, para el número 12.31 serían, entre otras:
12.31e0
1231e-2
123.1e-1
1.231e1
0.1231e2
0.01231e3
La representación de números fraccionarios que necesita de una menor cantidad de dígitos en notación científica, es aquella que utiliza un punto decimal después de la primera cifra significativa de la mantisa. Esta forma de representación se denomina normalizada (el resto de formas posibles se denominan subnormales). En el caso del número anterior, la notación normalizada sería: 1.231e1.
Nota: observe que en esta forma el exponente es mínimo, y representa la utilización de la máxima cantidad de cifras significativas en la mantisa, de forma que para una cantidad de cifras determinada, es la que permite mayor precisión.
Según lo anterior, la mantisa m de la
forma normalizada de un número distinto de cero, puede expresarse como suma
de una parte entera j y otra fraccionaria f,
m = j + f. Siendo j
un dígito decimal distinto de cero (1-9), y f una
cantidad menor que la unidad denominada fracción
decimal. De forma el número puede ser expresado mediante:
V = ± 0 (j + f) 10c §7.1.1a
En el caso del ejemplo esta representación sería: + (1+ 0.231) 101.
Nota: cuando el número está representado en binario la mantisa también puede ser representada en la forma m = j + f, siendo ahora j un dígito binario distinto de cero (que solo puede ser 1), el denominado bit-j. Desde luego f sigue siendo una cantidad menor que la unidad, aunque en este caso representada en binario (una fracción binaria). Si asumimos que la representación está siempre precedida de un 1, este bit puede suponerse implícito, y ocupar su posición para expresar un bit adicional de la fracción. Esta representación se denomina de significando normalizado y supone que solo se almacena la fracción decimal f de la mantisa (como puede ver, se trata de aprovechar al máximo el espacio disponible).
La expresión binaria equivalente a la anterior (§7.1.1a) es:
V = ± 0 (1+ f) 2c §7.1.1b
§3.2 Representación binaria
La informática, que en sus comienzos estaba nutrida por profesionales de otras disciplinas técnicas y científicas, adoptó una variación de la notación científica para representación interna (binaria) de las cantidades fraccionarias. Por esta razón, es costumbre que los números fraccionarios sean denominados de coma o punto flotante [1] ("floating-point") y a las operaciones aritméticas realizadas con ellos, operaciones de punto flotante FLOP ("FLoating -point- OPeration").
Para los números de "punto flotante", se ha asignando un bit para el signo; un cierto número de bits para representar el exponente y el resto para representar la parte más significativa del número (la mantisa), aunque en este caso, la característica no se refiere a una potencia de diez sino de dos. Es decir: un valor V puede ser representado por su mantisa m y su característica c mediante: V = m . 2c.
Así pues, la representación binaria de los números fraccionarios utiliza tres componentes:
-
Signo S es un número binario de un bit representando el signo (0 == positivo, 1 == negativo). Generalmente es el bit más significativo (de la izquierda).
-
Exponente c es un número binario representando la potencia de 2 por la que hay que multiplicar la mantisa. Cuanto mayor pueda ser este exponente, mayor será el valor absoluto del mayor número que puede ser representado.
-
Mantisa m es un número binario que representa las cifras significativas del número. Por supuesto, cuanto mayor sea la precisión deseada (más cifras significativas conocidas), mayor debe ser el espacio destinado a contener esta parte.
Consideramos los bits numerados de derecha a izquierda, de 0 a N-1 (siendo N el número total de bits que se utilizará en la representación). El signo está representado por el último bit (bit N-1). A continuación le siguen los bits destinados al significando y finalmente los del exponente. Si se destinan e bits para contener al exponente (representados E), y m para contener la mantisa (representados M), el esquema de almacenamiento es:
<--------------- N --------------> Espacio total de almacenamiento (bits)
S EEEEEEEE MMMMMMMMMMMMMMMMMMMMMMM Distribución
1 <-- e -> <---------- m --------> Longitud de campos
| | | | |
N-1m+e m m-1 0 Numeración de los bits
Es interesante observar que los desplazamientos ("Shift") izquierdo
o derecho (![]() 4.9.3)
de los bits de la mantisa, equivalen respectivamente a multiplicar o
dividir por dos su valor, lo que podría compensarse disminuyendo o aumentando
el valor del exponente en una unidad. Para evitar ambigüedades se
recurre a la normalización ya señalada
4.9.3)
de los bits de la mantisa, equivalen respectivamente a multiplicar o
dividir por dos su valor, lo que podría compensarse disminuyendo o aumentando
el valor del exponente en una unidad. Para evitar ambigüedades se
recurre a la normalización ya señalada ![]() ,
de forma que se minimiza el valor del exponente, y cualquier valor V (distinto
de cero) puede ser representado mediante la fracción normalizada f
de su mantisa (f # 0), con lo que puede ser representado en la forma:
,
de forma que se minimiza el valor del exponente, y cualquier valor V (distinto
de cero) puede ser representado mediante la fracción normalizada f
de su mantisa (f # 0), con lo que puede ser representado en la forma:
V = ± 2c (1 + f)
 |
Desgraciadamente no existe una absoluta unidad de criterio
respecto a los detalles. Según el Estándar, la representación (interna) y rango de
valores de los números fraccionarios depende del compilador
(![]() 2.2.4).
Cada implementación C++ es libre para definir los detalles. Por ejemplo, que espacio dedica a almacenar el exp,
y cuanto a la mantisa; como se representa el cero, Etc [2]. Como consecuencia, existen diferencias
en algunos aspectos del comportamiento de los compiladores que pueden llegar
a ser cruciales. Por ejemplo, cuando presentan errores de overflow o undeflow.
2.2.4).
Cada implementación C++ es libre para definir los detalles. Por ejemplo, que espacio dedica a almacenar el exp,
y cuanto a la mantisa; como se representa el cero, Etc [2]. Como consecuencia, existen diferencias
en algunos aspectos del comportamiento de los compiladores que pueden llegar
a ser cruciales. Por ejemplo, cuando presentan errores de overflow o undeflow.
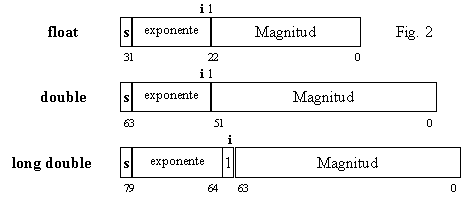
Nota: el compilador C++Builder utiliza tres tamaños distintos
para los números
fraccionarios de 32, 64 y 80 bits respectivamente, según el formato de
la IEEE ![]() . La
representación interna es la indicada en la figura 2.
. La
representación interna es la indicada en la figura 2.
§3.2.1 Problemas de la
representación binaria de las cantidades fraccionarias
La representación binaria de punto flotante utilizada en los computadores digitales, es muy eficiente y se adapta bastante bien a la mayoría de las circunstancias, especialmente en cálculos técnicos y científicos (aritmética de punto flotante). Sin embargo, no está exenta de problemas, derivados del hecho de que -como hemos señalado al principio del capítulo- las posibilidades (finitas) de representación del ordenador no pueden cubrir la totalidad (infinita) de los números reales. Esta dificultad es especialmente molesta en los cálculos denominados "de gestión", "comerciales" o "financieros" que utilizan números fraccionarios de base 10. Por ejemplo cálculos de precios, de conversión de moneda o del resultado de varias pesadas. Este tipo de aplicaciones utilizan (o deberían utilizar) lo que se denomina aritmética decimal (que realizamos habitualmente con un papel y un lápiz) en la que, por ejemplo, 111.567 - 111 = 0.567.
Cuando en los programas C/C++ se utilizan variables fraccionarias para almacenar este tipo de variables (números fraccionarios de base 10), se presentan problemas que, en principio, suelen desconcertar al principiante. Como botón de muestra, incluimos el mensaje de un usuario en un foro de Visual C++, titulado "A very serious bug in MS Visual C++" (evidentemente el usuario está bastante desconcertado con los resultados obtenidos y como suele ser normal en estos casos, echa la culpa al compilador).
Try the next code:
double a=111.567, b=111, c;
c=a-b;
// and you will receive
//
// a=111.56699999999999
// b=111.00000000000000
// c=0.56699999999999307
//
// instead => a=111.567, b=111, c=0.567;
I found more fractional numbers that show a similar error.
The problem is that the fractional numbers and their actions can not be produced otherwise.
I try this example in all MS Visual C/C++ compilers from version 6.0 to version 2008 and the bug appears everywhere.
Regards.
Mejor que puedan hacerlo mis palabras, en la página Decimal Arithmetic FAQ de Mike Cowlishaw
de IBM, encontrará el lector una amplia explicación del porqué de estos aparentemente erróneos
resultados. Como síntesis indicaremos aquí que, para prevenir estos
problemas, algunos lenguajes incluyen un tipo especial de variable
"decimal" y funciones y operadores específicos que permiten realizar cálculos de
aritmética decimal.
En lo que respecta a C++, debido a sus orígenes "científicos", por
el momento no dispone de forma nativa de ningún tipo decimal por lo que
las aplicaciones que necesitan de estos de cálculos deben recurrir a
librerías específicas.
Nota: aunque por el momento (Septiembre 2008) el lenguaje C++ no dispone de ningún tipo decimal, el comité de estandarización ya está trabajando en una especificación que se ajusta al estándar IEEE 754R (ver Decimal Types for C++). Seguramente se definirán tres tipos decimales de punto flotante de 32, 64 y 128 bits respectivamente. También es previsible que, del mismo modo que los procesadores modernos incluyen unidades hardware (FPU) para cálculos con números de punto flotante de codificación binaria, en un futuro próximo se implementen también en hardware unidades para cálculos con números de punto flotante de codificación decimal, ya que las rutinas software actuales para tratar la aritmética decimal son considerablemente más lentas que las de aritmética binaria.
§3.3 El Estándar IEEE 754
En 1985, el IEEE (Institute of Electrical and Electronics Engineers
![]() IEEE Standards Site) publicó la norma IEEE 754. Una especificación relativa a la
precisión y formato de los números de "punto flotante". Incluye una lista de las operaciones que
pueden realizarse con dichos números, entre las que se encuentran las cuatro
básicas: suma, resta, multiplicación, división. Así como el resto, la raíz cuadrada y diversas conversiones. También incluye el
tratamiento de circunstancias excepcionales, como manejo de números infinitos y valores no numéricos.
IEEE Standards Site) publicó la norma IEEE 754. Una especificación relativa a la
precisión y formato de los números de "punto flotante". Incluye una lista de las operaciones que
pueden realizarse con dichos números, entre las que se encuentran las cuatro
básicas: suma, resta, multiplicación, división. Así como el resto, la raíz cuadrada y diversas conversiones. También incluye el
tratamiento de circunstancias excepcionales, como manejo de números infinitos y valores no numéricos.
Nota: en Junio de 2008 se aprobó una revisión de dicho Estándar, conocido como IEEE 754R, que incluye recomendaciones para la aritmética de punto flotante de codificación decimal. La explicación que sigue se refiere exclusivamente a la codificación de números de punto flotante de codificación binaria (versión inicial del estándar).
Dado que la mayoría de compiladores utilizan este formato para la representación de los números fraccionarios, es más que probable que el informático se tope con ellos en alguna ocasión, por lo que dedicaremos unas líneas a describir sus características principales [7].
En realidad, la adopción de este estándar por parte de los compiladores se debe a que el hardware que los sustenta también lo sigue. De hecho, esta es la representación interna utilizada por los procesadores, ya que en la actualidad (2002) prácticamente el 100% de las máquinas que se fabrican siguen el Estándar en lo que se refiere al tratamiento y operación de los números de "punto flotante".
El proceso de estandarización de las operaciones de punto flotante comenzó paralelamente al desarrollo por Intel (1976) de lo que serían los coprocesadores aritméticos 8087. A partir de entonces podía asegurarse que X + (Y + Z) proporcionaría el mismo resultado que (X + Y) + Z con cualquier compilador y cualquier terna de números. No olvidemos que es precisamente a partir de la aparición de los coprocesadores matemáticos, cuando la realización de operaciones con números fraccionarios se encomiendan al silicio (hardware), en vez de a rutinas software que, hasta entonces, eran específicas de cada compilador y cada plataforma [9].
Los coprocesadores matemáticos, denominados también FPUs (Floating-Pount Units) comenzaron siendo circuitos integrados (opcionales) que se insertaban en la placa base junto al procesador principal [4]. Por ejemplo los 8087, 80287 y 80387 de Intel (este último fue el primero que proporcionó soporte completo para la versión final del Estándar). A partir del 80486, Intel incorporó el coprocesador matemático junto con el principal, con lo que su existencia dejó de ser opcional y se convirtió en estándar. Estas "unidades de punto flotante" no solo realizan las operaciones aritméticas básicas (suma resta, multiplicación y división). También incluyen operaciones como la raíz cuadrada, redondeo, resto, y funciones trascendentes como seno, coseno, tangente, cotangente, logaritmación y exponenciación.
§3.3.1 Formatos
En lo referente a la representación binaria de los números, el Estándar utiliza tres formatos denominados de precisión simple (equivalente al float C++); doble (equivalente al double) y extendida (que podría corresponder al long double), aunque existe un cuarto, denominado de cuádruple precisión, no contemplado en la norma que es también un estándar de facto. Los tamaños son los siguientes:
| Precisión | Bytes |
bits |
| Simple | 4 |
32 |
| Doble | 8 |
64 |
| Extendida | >= 10 |
>= 80 |
| Cuádruple | 16 |
128 |
En todos los casos se utilizan tres campos para describir el número: El signo
S, el exponente k y el
significando (mantisa) n, que se almacenan en ese orden en memoria (no en los registros del procesador).
-
El signo S, se almacena como es usual en un bit (0 significa positivo, 1 negativo).
-
El exponente k se almacena en forma de un número binario con signo según una regla que, como veremos a continuación, depende del rango y del formato.
-
El significando n se almacena en forma normalizada, salvo cuando se representan significados especiales (ver a continuación).
El esquema de la distribución utilizada para los de simple y doble precisión es el indicado.
Como veremos a continuación, la interpretación de los patrones de bits contenidos en el exponente
y en el significando sigue reglas algo complicadas. El motivo es que del espacio total de posibilidades se
han reservado algunas para significados especiales y circunstancias excepcionales, que es necesario
considerar para prevenir los errores e imprecisiones aludidas al principio del capítulo
![]() .
Por ejemplo, se considera la existencia de valores especiales: +Infinito; -Infinito; NaN ("Not a Number") y una
representación especial para el valor cero, lo que ha obligado a definir reglas especiales de aritmética cuando estos valores
intervienen en operaciones con valores normales o entre ellos
.
Por ejemplo, se considera la existencia de valores especiales: +Infinito; -Infinito; NaN ("Not a Number") y una
representación especial para el valor cero, lo que ha obligado a definir reglas especiales de aritmética cuando estos valores
intervienen en operaciones con valores normales o entre ellos
![]() . A lo anterior se añade que existen dos tipos de
representación para los valores no especiales, cada uno con sus reglas; son las denominadas formas normalizadas y
subnormales.
. A lo anterior se añade que existen dos tipos de
representación para los valores no especiales, cada uno con sus reglas; son las denominadas formas normalizadas y
subnormales.
Empezaremos por la representación de los significados especiales.
§3.3.2 Significados especiales
-
Definición del cero: puesto que el significando se supone almacenado en forma normalizada
 ,
no es posible representar el cero (se supone siempre precedido de un 1).
Por esta razón se convino que el cero se representaría con valores 0 en el
exponente y en el significando. Ejemplo:
,
no es posible representar el cero (se supone siempre precedido de un 1).
Por esta razón se convino que el cero se representaría con valores 0 en el
exponente y en el significando. Ejemplo:0 00000000 00000000000000000000000 = +0
1 00000000 00000000000000000000000 = -0
 Observe que en estas condiciones el bit de signo S
aún permite distinguir +0 de -0. De hecho, el compilador lo hace así, permitiendo distinguir divisiones por
cero con resultado +4 y -4
Observe que en estas condiciones el bit de signo S
aún permite distinguir +0 de -0. De hecho, el compilador lo hace así, permitiendo distinguir divisiones por
cero con resultado +4 y -4  . Sin embargo el Estándar establece que al comparar ambos
"ceros" el resultado debe indicar que son iguales.
. Sin embargo el Estándar establece que al comparar ambos
"ceros" el resultado debe indicar que son iguales. -
Infinitos: se ha convenido que cuando todos los bits del exponente están a 1 y todos los del significando a 0, el valor es +/- infinito (según el valor S). Esta distinción ha permitido al Estándar definir procedimientos para continuar las operaciones después que se ha alcanzado uno de estos valores (después de un overflow). Ejemplo:
0 11111111 00000000000000000000000 = +Infinito
1 11111111 00000000000000000000000 = -Infinito
-
Valores no-normalizados (denominados también "subnormales"). En estos casos no se asume que haya que añadir un 1 al significado para obtener su valor. Se identifican porque todos los bits del exponente son 0 pero el significado presenta un valor distinto de cero (en caso contrario se trataría de un cero). Ejemplo:
1 00000000 00100010001001010101010
-
Valores no-numéricos: Denominados NaN ("Not-a-number"). Se identifican por un exponente con todos sus valores a 1, y un significando distinto de cero. Existen dos tipos QNaN ("Quiet NaN") y SNaN ("Signalling NaN"), que se distinguen dependiendo del valor 0/1 del bit más significativo del significando. QNaN tiene el primer bit a 1, y significa "Indeterminado", SNaN tiene el primer bit a 0 y significa "Operación no-válida". Ejemplo:
0 11111111 10000100000000000000000 = QNaN
1 11111111 00100010001001010101010 = SNaN
§3.3.3 Significados normales
La representación de números no incluidos en los casos especiales (distintos de cero que no sean infinitos ni valores no-numéricos), sigue reglas distintas según la precisión y el tipo de representación (normal o subnormal).
Para calcular el valor V
de un número binario IEEE 754 de exponente E y
mantisa M, debe recordarse que esta
última representa una fracción
binaria (no decimal ;-) en notación normalizada
![]() . Es decir, hay que
sumarle una unidad. En estas condiciones, si por ejemplo, el contenido
de la mantisa es 0.254 se supone que M = 1 + 0.254. Por su parte el
cálculo de la fracción binaria es análogo al de la fracción decimal. Recordemos que la fracción decimal 1304 (0.1304) equivale a 1/101
+ 3/102 + 0/103 + 4/104. Del mismo
modo, la fracción binaria 1101 (0.1101) equivale a 1/21 + 1/22
+ 0/23 + 1/24 = 0.8125.
. Es decir, hay que
sumarle una unidad. En estas condiciones, si por ejemplo, el contenido
de la mantisa es 0.254 se supone que M = 1 + 0.254. Por su parte el
cálculo de la fracción binaria es análogo al de la fracción decimal. Recordemos que la fracción decimal 1304 (0.1304) equivale a 1/101
+ 3/102 + 0/103 + 4/104. Del mismo
modo, la fracción binaria 1101 (0.1101) equivale a 1/21 + 1/22
+ 0/23 + 1/24 = 0.8125.
Teniendo en cuenta estas observaciones, el valor decimal V de una representación binaria estándar, puede calcularse mediante las siguientes fórmulas:
Nota: en las fórmulas que siguen puede suponerse sustituido el signo ±
por la expresión (-1)S. Donde S es el valor del bit de signo; cero
si es positivo y 1 si es negativo.
Si es un problema real, en el que es preciso calcular el valor correspondiente
a un binario que sigue el estándar (por ejemplo, los datos recibidos de un
instrumento de medida), además de las consideraciones anteriores, también
hay que tener en cuenta el orden ("Endianness") en que pueden
recibirse los datos (![]() 2.2.6a).
2.2.6a).
§3.3.3a Simple precisión, representación normalizada:
V == ± (1 + M) 2E-127
Es evidente que en estos casos E es un número tal que 0 < E < 255 (28 - 2 posibilidades), ya que en caso contrario se estaría en alguno de los significados especiales (todos los bits del exponente a 0 o a 1). Así pues, E se mueve en el intervalo 1 a 254 (ambos inclusive) Al restarle 127 queda un rango entre 2-126 y 2127.
Ejemplos:
0 00001100 11010000000000000000000
Signo = +; E = 12; M = 1/21 + 1/22 + 0/23 + 1/24 + 0 + 0 + ... = 0.8125
V = + (1 + 0.8125) 212-127 = 1.8125 · 2-115 = 4.3634350 · 10-35
1 10001101 01101000000000000000000
Signo = -; E = 141; M = 0/21 + 1/22 + 1/23 + 0/24 + 1/25 + 0 + ... = 0.40625
V = - (1 + 0.40625) 2141 = - 1.40625 · 214 = - 23040
§3.3.3b Simple precisión, representación subnormal:
V == ± (0 + M) 2-127
Como se ha señalado ![]() ,
en estos casos es E = 0, y M
es distinto de cero. La operatoria es análoga al caso anterior.
,
en estos casos es E = 0, y M
es distinto de cero. La operatoria es análoga al caso anterior.
Ejemplo:
0 00000000 11010000000000000000000
Signo = +; E = 0; M = 1/21 + 1/22 + 0/23 + 1/24 + 0 + 0 + ... = 0.8125
V = + 0.8125 · 2-127 = 4.77544580 · 10-39
§3.3.3c Doble precisión, representación normalizada:
V == ± (1 + M) 2E-1023
En estos casos es 0 < E < 2047. En caso contrario se estaría en alguno de los significados especiales (todos los bits del exponente a 0 o a 1). La operatoria es análoga a la de simple precisión, con la diferencia de que en este caso se dispone de más espacio para representar la mantisa M y el exponente E (52 y 11 bits respectivamente).
§3.3.3d Doble precisión, representación subnormal:
V == ± (0 + M) 2-1023
En estos casos es E = 0, y M es distinto de cero. La operatoria es análoga a la señalada en casos anteriores.
§3.3.4 Conversor automático de formatos
Con objeto de facilitar al lector la realización de algunos
ejemplos que le permitan terminar de comprender y comprobar estas reglas, en la página
adjunta se incluye un convertidor automático de formatos que permite
introducir un número en formato decimal (incluso en notación científica), y
comprobar el aspecto de su almacenamiento binario según el Estándar IEEE 754
en simple y doble precisión ( ![]() Conversor).
Conversor).
Nota: en la librería de ejemplos (![]() 9.4.1)
se incluye un programa C++ que realiza la misma conversión que el anterior
(realizado en javascript), aunque está limitado a la representación de
números en precisión simple.
9.4.1)
se incluye un programa C++ que realiza la misma conversión que el anterior
(realizado en javascript), aunque está limitado a la representación de
números en precisión simple.
§3.3.5 Operaciones con números especiales
La tabla adjunta establece las reglas que, según el Estándar IEEE 754, rigen las operaciones en que intervienen magnitudes de significado especial.
| Operación: | Resultado |
| cualquiera con NaN | NaN |
| n / ± Infinito | ± 0 |
| ± Infinito * ±Infinito | ± Infinito |
| Infinito + Infinito | Infinito |
| Infinito - Infinito | NaN |
| ± Infinito * 0 | NaN |
| ± Infinito / ± Infinito | NaN |
| ±0 / ±0 | NaN |
| ±n / ±0 | ± Infinito |
§3.3.6 Rango de la representación IEEE 754
Exceptuando los valores especiales infinitos, está claro que para la simple precisión, los valores mínimos y máximos que pueden representarse de forma estandarizada son:
Vmin = - (0 + M) 2-127, donde M sea el valor mínimo de la mantisa distinto de cero. Su representación es
1 00000000 00000000000000000000001
Traducción:
Signo = -
E = 0
M = 1/223 = 2-23 = 1.19209289551 · 10-7
Vmin = 2-23 · 2-127 = 2-150 = 7.00649232163 · 10-46
En la práctica solo se consideran las representaciones normales, de forma que la forma normal más pequeña corresponde a la siguiente representación binaria:
1 00000001 00000000000000000000001
Traducción:
Signo = -
E = 1
M = 1/223 = 2-23
Vmin = -(1 + 2-23) 21-127 = -(1 + 2-23) 2-126 = -1.17549449 · 10-38
Es significativo que el próximo valor en escala ascendente es
1 00000001 00000000000000000000010
Signo = -;
E = 1
M = 1/222 = 2-22
V = -(1 + 2-22) 2-126
La diferencia entre ambos es: Imin = V - Vmin = 2-22 - 2-23 = 1.192092 · 10-7, lo que representa algo más de una parte en 10 millones. Es importante recordar que esta será la mejor precisión que podrá alcanzarse en los procesos con números de coma flotante de simple precisión. En la práctica la precisión alcanzada será aún menor, dependiendo de la suerte que tengamos y del número de operaciones encadenadas que se hayan realizado (los errores pueden ser aleatorios -que tienden a anularse entre sí- o acumulativos).
El valor máximo en la representación normal, corresponde a la forma binaria
0 11111110 11111111111111111111111
Signo = +
E = 254
M = 1/21 + 1/22 + ... + 1/223 = 0.9999999999
Vmax = (1 + 0.999999) 2254-127 = (1.99999999) 2127 = 3.40282346 · 1038
.
[0] Los números reales comprenden los racionales e irracionales. Números racionales son los que se pueden escribir en forma de entero o quebrado de dos enteros (2/3, 8/5, Etc.) Así pues, incluyen los enteros, tanto los naturales (positivos) como los negativos, y los fraccionarios (positivos y negativos), siempre que estos tengan un número finito de cifras decimales, o formen una fracción decimal periódica pura o mixta.
Por su parte, los números irracionales o inconmensurables, no son enteros ni fraccionarios, es decir, no se pueden representar mediante una fracción de enteros, y su representación decimal consta de infinitas cifras que no forman periodo. Por ejemplo el número e (base de los logaritmos Neperianos), la raíz cuadrada de 2, el número pi, Etc.
[1] La cuestión de "coma" o "punto" es un localismo dependiente de la forma de representar el signo decimal en los números fraccionarios. Aunque tradicionalmente en España se ha utilizado la coma para representar la posición decimal y el punto para los grupos de miles, en otros países de habla Española se utiliza a la inversa por influencia de la cultura USA.
[2] Por ejemplo: las máquinas VAX de DEC (Digital Equipment Corporation) utilizaban para los números de coma flotante dos formatos distintos, con 8 y 11 bits para el valor de exp, dependiendo de la precisión necesaria. Estos valores fueron adoptados más tarde por el estándar.
[3] Esta limitación es más acusada en el sistema binario, ya que para representar cualquier cantidad en este
sistema, los números necesitan de más dígitos que su representación decimal
(![]() 0.1).
0.1).
[4] Puesto que en los primeros modelos la existencia del coprocesador era opcional, en caso de ausencia se recurría a un truco: Se generaba una interrupción y se invocaba una rutina software que emulaba el comportamiento del hadrware ausente. Por supuesto, al costo de una velocidad de proceso incomparablemente más lenta.
[5] Por esta razón a la mantisa se la denomina también significando (especialmente en la literatura inglesa).
[6] "The Intel Architecture Software Developer’s Manual", Volume 1: Basic Architecture (Order Number 243190) es parte de una serie de tres volúmenes que describen la arquitectura y ambiente de programación de todos los procesadores de arquitectura Intel. Los otros dos volúmenes de la serie son:
The Intel Architecture Software Developer’s Manual, Volume 2: Instruction Set Reference (Order Number 243191).
The Intel Architecture Software Developer’s Manual, Volume 3: System Programming Guide (Order Number 243192).
Nota: Para su localización buscar en el sitio de Intel ![]() www.intel.com introduciendo el número de orden en el buscador.
www.intel.com introduciendo el número de orden en el buscador.
[7] La información al respecto que puede obtenerse en la Red es muy
abundante. Una de las mejores referencias es el documento "Lecture Notes on the Status of
IEEE Standard 754 for Binary Floating-Point Arithmetic" del profesor W.
Kahan, del departamento de Ingeniería Eléctrica y Ciencias de la Computación
de la Universidad de California en Berkeley: ![]() www.cs.berkeley.edu/~wkahan/ieee754status/IEEE754.PDF.
Viene avalado por la autoridad del autor, ya que junto con Jerome Coonen y Harold Stone prepararon el borrador denominado K-C-S
(iniciales de sus autores), que posteriormente dio origen al estándar IEEE 754.
www.cs.berkeley.edu/~wkahan/ieee754status/IEEE754.PDF.
Viene avalado por la autoridad del autor, ya que junto con Jerome Coonen y Harold Stone prepararon el borrador denominado K-C-S
(iniciales de sus autores), que posteriormente dio origen al estándar IEEE 754.
El Doctor Christopher Vickery, del departamento de Ciencias de la Computación del Queens College de NY, tiene
una página con abundantes referencias al Estándar: ![]() http://babbage.cs.qc.edu/courses/cs341/IEEE-754references.html.
http://babbage.cs.qc.edu/courses/cs341/IEEE-754references.html.
[8] A título de ejemplo incluimos un párrafo tomado del manual de referencia de MySQL, una popular base de datos relacional: "All data is stored with the low byte first. This makes the data machine and OS independent. The only requirement is that the machine uses two's-complement signed integers (as every machine for the last 20 years has) and IEEE floating-point format (also totally dominant among mainstream machines)".
[9] Como anécdota puedo contaros que las primeras "Librerías matemáticas" que cayeron en mis manos, unas rutinas HP para cálculo aritmético y trascendente, venían en cinta perforada y acompañadas de una especie de "Molino de oraciones" para volver a enrollarlas - El modelo de cinta perforada de HP era enrollada, como una serpentina. Otros fabricantes utilizaban el formato plegado, que resultaba más cómodo-.