Subir
4.3.6 Matrices de matrices
§1 Sinopsis:
Las matrices de matrices (matrices multidimensionales), son simplemente matrices cuyos elementos son otras matrices. C++ no
dispone de elementos incluidos en el propio lenguaje para manejar matrices [2]; mucho menos matrices
multidimensionales. Sin embargo, la Librería Estándar (
5) proporciona potentes recursos para manejo de vectores y matrices. En concreto, existen una serie de
clases predefinidas para este fin: vector, list, valarray, string, etc., dotadas de interfaces muy
completas y cómodas para el programador.
El propio creador del C++ (
TC++PL §C.7.2 ) reconoce que el manejo de matrices multidimensionales "a pelo", tal
como están implementadas en el lenguaje, son una importante fuente de errores y confusión, especialmente para el principiante.
Aparte de una posible pesadilla para futuros mantenedores de tales programas, a no ser que estén cuidadosamente
documentados.
En consecuencia, aconseja utilizar en lo posible los recursos ofrecidos por la Librería Estándar.
No obstante lo anterior, incluso para manejar las Librerías, es imprescindible un mínimo conocimiento de las capacidades incluidas en el lenguaje: "cómo considera en realidad C++ las matrices multidimensionales"; aspecto este al que dedicamos el resto del epígrafe.
§2 Declaración
Las matrices multidimensionales son matrices de matrices (matrices cuyos elementos son matrices):
int dias[2][12] = {
{31,28,31,30,31,30,31,31,30,31,30,31},
{31,29,31,30,31,30,31,31,30,31,30,31} };
char lista[5][4] = { "Cat", "Bar", "Cab", "Lab", "Tab" };
§3 Sintaxis:
La forma de declararlas es mediante una serie de expresiones entre corchetes [1]:
tipoX etiqueta [<expr-c1>][<expr-c2>]...[exp-cn]
Ejemplo:
int ai[2][3+1][6];
Comentario
El resultado de las expresiones <expr-c> representan el tamaño de cada submatriz, y deben reducirse a enteros positivos (unsigned int) distintos de cero. Cada submatriz es una "dimensión" de la matriz total. En el caso de matrices de dos dimensiones, <expr-c1> y <expr-c2> se denominan respectivamente filas y columnas. En el caso de más de dos dimensiones, la expresión <expr-cn> se denomina sencillamente "dimensión-n".
El número total de elementos de una matriz de n dimensiones es el producto de los valores de todas las dimensiones. En el ejemplo anterior, la matriz ai tiene 2 x 4 x 6 = 48 elementos.
§4 Acceso mediante subíndices
Lo mismo que en el caso de matrices unidimensionales, existen dos formas para acceder los elementos de matrices multidimensionales: mediante subíndices y mediante punteros. En cuanto a la primera, la forma de designar un elemento es: a[f][c], el primer subíndice indica la fila y el segundo la columna.
Los elementos se almacenan por filas, de forma que el subíndice de la derecha (de columna) varía más rápidamente si los elementos se recorren en orden de almacenamiento. En realidad, una matriz bidimensional como dias, es para el compilador una matriz de una sola fila (dimensión) de elementos contiguos, en la que cada elemento es a su vez una matriz. En este caso una matriz de dos elementos, cada uno de los cuales es a su vez matriz de 12 elementos.
El razonamiento puede hacerse recursivo, de forma
que una matriz de n dimensiones es una matriz de una sola fila, cada uno de cuyos x1 elementos es a su vez una
matriz de una fila de x2 elementos, cada uno de los cuales...
Si aplicamos este razonamiento a una matriz m de enteros de tres dimensiones:
-
int m[X][Y][Z]; Es la declaración de la matriz;
-
m[a][b][c] Es un elemento de la matriz (en este caso un int)
-
m Es el identificador de la matriz. Para algunos efectos puede ser considerado identificativo de la matriz como un todo. Para otros efectos puede ser considerado como un puntero que señala al elemento m[0][0][0]: m == &m[0][0][0]
-
m[0][0][0] Es el primer elemento de la matriz
-
m[X-1][Y-1][Z-1] Es el último elemento.
§5 Posición de un elemento
Al tratar de punteros y matrices de una dimensión (
4.3.2), vimos que la posición Pi (contada en elementos
respecto al comienzo) del elemento m[ i ] de una matriz de elementos tipoX es simplemente
Pi = i.
En caso de una matriz bidimensional m[A][B], la posición Pa,b respecto del comienzo del elemento m[a][b] viene determinado por: Pa,b = ( a * B ) + b. Es decir: (fila x total de columnas) + columna.
En el caso del ejemplo anterior, el elemento dias[1][1] (número 29) está en la posición: P1,1 =
(1 * 12)+ 1 == 13. Lo que significa que, para alcanzar el almacenamiento del número 29, desde la posición inicial (número
31), hay que desplazarse internamente en la memoria el espacio correspondiente a 13 int. (ver demostración
4.3.6w1).
Por su parte, el elemento lista[3][0] (carácter 'L'), está en la posición P3,0 = (3 * 4) + 0 == 12 desde el carácter inicial 'C'. Recuerde que cada submatriz de lista es una cadena de 4 elementos, el último es el terminador de cadena "\0" (no representado).
El razonamiento puede ser extendido a la posición Pa,b,c..z de cualquier elemento
m[a][b][c]...[z] de una matriz multidimensional m[A][B][C]...[Z],
siendo sus dimensiones A, B, C... Z:
Pa,b,c...z == a · (B·C·D·E·.. ·Z) + b · (C·D·E·...·Z) + d · (D·E·...·Z) + .... + z §5.a
Nota: el punto · (aunque apenas visible) representa aquí el símbolo de multiplicar. Los términos B·C·D·E...Z representan productos de las dimensiones de la matriz.
§5.1 Una observación importante es que la
posición de un elemento no viene influenciada por el valor de la primera dimensión A (que no aparece en la
fórmula), lo que tiene cierta trascendencia cuando se trata de pasar matrices como argumento de funciones
( 4.3.8).
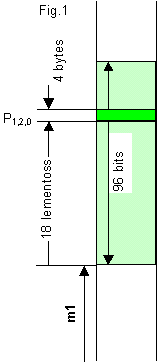
Desde este punto de vista, una matriz m1 definida como:
int m1[2][4][3];
tiene 2 x 4 x 3 = 24 elementos tipo int, cada uno de los cuales ocupa 4 bytes.
La matriz ocupa 24 x 4 = 96 bytes (
2.2.4). Su almacenamiento se esquematiza en la figura
1 (en su interior se ha representado la posición del elemento m1[1][2][0]). La posición de cualquier elemento
m1[a][b][c] viene determinada por la expresión:
Pa,b,c == a * (4*3) + b (3) + c == a * 12 + b * 3 + c
El elemento m1[0][0][0] está en la posición P0,0,0 == 0 * 12 + 0 * 3 + 0 == 0. El elemento m1 [1][2][0] en la posición P1,2,0 == 1 * 12 + 2 * 3 + 0 == 18, y el último elemento, m1[1][3][2] en la posición P1,3,2 == 1 * 12 + 3 * 3 + 2 == 23
§6 Acceso a elementos mediante punteros
El operador de elemento de matriz [ ] (
4.9.16) se define como:
<exp1>[exp2] ↔ *((exp1) + (exp2))
donde exp1 es un puntero y exp2 es un entero, o exp1 es un entero y exp2 es un puntero. Según esta definición la expresión del elemento a de una matriz m, m[a] sería equivalente a la expresión *(m + a).
§6.1 Hemos señalado
que en una matriz bidimensional m[A][B], cada
elemento m[a] de la primera (y en realidad única fila), es una matriz m1 de B elementos, en la
que el elemento m1[b] sería equivalente a *(m1 + b).
Sustituyendo en esta última fórmula m1 por su equivalente, se tiene:
m1[b] ↔ m[a][b] ↔ *( *( m + a ) + b )
El razonamiento puede extenderse a matrices de cualquier número de dimensiones
(
4.9.16). De forma que en general, se tiene la siguiente serie de
equivalencias:
Matriz de una dimensión: m[a] == *( m + a )
Matriz de 2 dimensiones: m[a][b] == *( *( m + a ) + b )
Matriz de 3 dimensiones: m[a][b][c] == *( *( *( m + a ) + b ) + c )
Matriz de 4 dimensiones: m[a][b][c][d] == *( *( *( *( m + a ) + b ) + c )+ d)
etc.
Ejemplo:
char m[][5] = {{'a','e','i','o','u'},{'A','E','I','O','U'}};
cout << "Caracter " << m[1][3]; // -> Caracter O
cout << "Caracter " << *(*(m+1)+3); // -> Caracter O
int dia[][5][2] = { {{ 0, 1},{ 10, 11},{ 20, 21},{ 30, 31},{ 40, 41}},
{{100,101},{110,111},{120,121},{130,131},{140,141}} };
int a =0, b=2, c= 0;
cout << "dia [0,2,0] = " << *(*(*(dia+a)+b)+c); // -> dia [0,2,0] = 20
a= 0; b=3; c=1;
cout << "dia [0,3,1] = " << *(*(*(dia+a)+b)+c); // -> dia [0,3,1] = 31
a =1; b=2; c= 0;
cout << "dia [1,2,0] = " << *(*(*(dia+a)+b)+c); // -> dia [1,2,0] = 120
§6.2 Si nos referimos al primer elemento de una matriz de una, dos, tres, etc. dimensiones, las expresiones
anteriores se reducen a:
Matriz de una dimensión: m[0] == *( m + 0 ) == *m
Matriz de 2 dimensiones: m[0][0] == *( *( m + 0 ) + 0 ) == **m
Matriz de 3 dimensiones: m[0][0][0] == *( *( *( m + 0 ) + 0 ) + 0 ) == ***m
Matriz de 4 dimensiones: m[0][0][0][0] == *( *( *( *( m + 0 ) + 0 ) + 0 )+ 0) == ****m
etc.
§6.3 Si aplicamos el operador de referencia &
(
4.9.11) a cada lado de las relaciones de equivalencia anteriores, y
tenemos en cuenta que la dirección del primer elemento &m[0] es igual a la dirección de la matriz &m, y
que los operadores &* se anulan entre sí:
Matriz de una dimensión: &m[0] == &m == m §6.3a
Matriz de 2 dimensiones: &m[0][0] == &m == *m
Matriz de 3 dimensiones: &m[0][0][0] == &m == **m
Matriz de 4 dimensiones: &m[0][0][0][0] == &m == ***m
etc.
La equivalencia §6.3a referida a matrices unidimensionales ya la habíamos visto anteriormente
( 4.3.2) enunciada
como: el identificador de una matriz es considerado un puntero a su primer elemento.
Ejemplo:
char m1[] = {'a','e','i','o','u'};
cout << "Caracter " << *m1; // -> Caracter a
cout << "Caracter " << m1[0]; // -> Caracter a
char m2[][5] = {{'a','e','i','o','u'},{'A','E','I','O','U'}};
cout << "Caracter " << **m2; // -> Caracter a
cout << "Caracter " << m2[0][0]; // -> Caracter a
§6.4 La comprensión del significado de las relaciones §6.1 a §6.3, es de la mayor trascendencia para el manejo de
matrices (especialmente multidimensionales). Pueden ser enunciadas de varias formas, aunque en el fondo todas son equivalentes.
Por ejemplo, las relaciones §6.3 pueden ser expresadas diciendo: la dirección del primer elemento de una matriz puede obtenerse
de la siguiente forma:
Matrices unidimensionales: mediante su identificador m.
Matrices bidimensionales: mediante la indirección del identificador *m.
Matrices tridimensionales: mediante la doble indirección del identificador **m.
Matrices n-dimensionales: mediante la n-1 indirección del identificador.
§6.5 Teniendo en cuenta que cualquiera que sean las dimensiones de una matriz, el tipo de la dirección a uno de
sus elementos es tipoX* (puntero-a-tipoX), las equivalencias contenidas en los enunciados anteriores, pueden traducirse
en afirmar que el tipo del identificador m de una matriz de objetos tipoX es:
Matrices unidimensionales: tipoX* (puntero-a-tipoX).
Matrices bidimensionales: tipoX** (puntero-a-puntero-a-tipoX).
Matrices tridimensionales: tipoX*** (puntero-a-puntero-a-puntero-a-tipoX).
etc.
Expresado en otras palabras:
| Declaración | Descripción de m | Tipo de m | Descripción del tipo |
| tipoX m[a]; | Matriz unidimensional de objetos tipoX | tipoX* | Puntero-a-tipoX |
| tipoX m[a][b]; | Matriz bidimensional de objetos tipoX | tipoX** | Puntero-a-puntero-tipoX |
| tipoX m[a][b][c]; | Matriz tridimensional de objetos tipoX | tipoX*** | Puntero-a-puntero-a-puntero-tipoX |
| Etc. |
Ver comentario más extenso respecto de estas afirmaciones:
( 4.3.6a2)
Inicio.[1] Las expresiones con comas, del tipo m[x, y, z], utilizadas en otros lenguajes para representar elementos de matrices, no están permitidas en C++.
[2] Nos referimos a matrices como un todo. En cambio si se dispone de instrumentos para manejo de "elementos" de matrices. Existen no obstante, algunas excepciones notables. Por ejemplo, algunos casos de inicialización, donde son posibles sentencias del tipo:
int m[5] = { 'A','E','I','O','U'};
Ver en página siguiente "Iniciación conjunta"